1.20. Illustrate the division algorithm for m = 22, n =
11; m = 33, n = 45; m = 277,
n = 4.
1.21. Prove the existence part of the Division Algorithm. (Hint: Given n and m,
how will you define q? Once you choose this q, then how is r chosen? Then show
that
0 ≤ r ≤ n − 1.)
1.22. Prove the uniqueness part of the Division Algorithm. (Hint: If nq + r = nq'
+ r',
then nq − nq' = r' − r. Use what you know about r and r' as part of your
argument that
q = q'.)
1.23. Theorem. Let a, b, and n be integers with n > 0. Then a ≡ b (mod n) if and
only if a and b have the same remainder when divided by n. Equivalently, a ≡ b
(mod n) if
and only if when 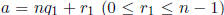 and
and
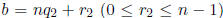 , then
, then
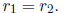
Definitions.
1. The greatest common divisor of two integers a and b is
the largest
integer d such that d|a and d|b. The greatest common divisor of two integers a
and b is
denoted gcd(a, b) or (a, b).
2. If gcd(a, b) = 1, then a and b are said to be relatively prime.
1.24. Question. Find (36, 22), (45,−15), (296,−88), (0, 256), and (15, 28).
1.25. Theorem. Let a, n, b, r, and k be integers. If a = nb + r and k|a and k|b,
then
k|r.
1.26. Theorem. Let 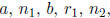 and
and
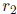 be integers. If
be integers. If
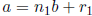 , then (a, b) =
, then (a, b) =
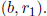 Similarly, if
Similarly, if
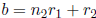 , then
, then 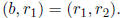
1.27. Question. As an illustration of the above theorem, note that
51 = 3 · 15 + 6
15 = 2 · 6 + 3
6 = 2 · 3 + 0.
Show that if a = 51 and b = 15, then (51, 15) = (6, 3) = 3.
1.28. Question (Euclidean Algorithm). Using the previous
theorem and the Division
Algorithm successively, devise a procedure for finding the greatest common
divisor of two
integers.
1.29. Use the Euclidean Algorithm to find (96, 112), (288, 166), and (175, 24).
1.30. Find integers x and y such that 175x + 24y = 1.
1.31. Theorem. Let a and b be integers. The greatest common divisor of a and b
equals
1 (i.e., (a, b) = 1) if and only if there exist integers x and y such that ax +
by = 1.
(Note: This theorem is an ‘if and only if’ theorem, so you must prove two
theorems: (1) If
(a, b) = 1, then there exist integers x and y such that ax + by = 1. And (2) If
there exist
integers x and y with ax + by = 1, then (a, b) = 1. The hint for the first part
is to use the
Euclidean Algorithm. Do some examples by taking some pairs of relatively prime
integers,
doing the Euclidean Algorithm, and seeing how to find the x and y. It is a good
idea to start
with an example where the Euclidean Algorithm takes just one step , then do an
example
where the Euclidean Algorithm takes two steps, then three steps, then look for a
general
procedure.)
1.32. Theorem. For any integers a and b, there are integers x and y such that
ax+by =
(a, b).
1.33. Theorem. Let a, b, and c be integers. If a|bc and (a, b) = 1, then a|c.
Theorems 1.30 and 1.31 begin to address the question : Given integers a, b, and
c, when
do there exist integers x and y that satisfy the equation ax+by = c? When we
seek integer
solutions to an equation , the equation is called a Diophantine equation.
1.34. Question. Suppose there is a solution to the linear Diophantine equation
ax +
by = c. What condition does c satisfy in terms of a and b ?
1.35. Question. Make a conjecture by completing the following theorem statement.
Conjecture. Given integers a, b, and c, there exist integers x and y that
satisfy the equation
ax + by = c if and only if  . Prove your
conjecture.
. Prove your
conjecture.
1.36. Theorem. Given integers a, b, and c, there exist integers x and y that
satisfy the
equation ax + by = c if and only if (a, b)|c.
1.37. Question. For integers a, b, and c, consider the
linear Diophantine equation
ax + by = c. Suppose integers
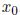 and
and
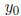 satisfy the equation,
that is,
satisfy the equation,
that is, 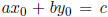 . What
. What
other values , 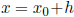 and
and
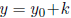 , also satisfy ax+by = c? Formulate a
conjecture that
, also satisfy ax+by = c? Formulate a
conjecture that
answers this question. Devise some numerical examples to ground your
exploration. For
example, 6(−2) + 15 · 2 = 18. Can you find other integers x and y such that 6x +
15y = 4?
How many other pairs of integers x and y can you find? Can you find infinitely
many other
solutions?
1.38. Question (Euler). A farmer lays out the sum of 1,770 crowns in purchasing
horses and oxen. He pays 31 crowns for each horse and 21 crowns for each ox.
What are
the possible numbers of horses and oxen that the farmer bought?
1.39. Theorem. Let a, b, c, 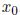 , and
, and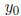 be integers such that
be integers such that 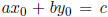 . Then
. Then
the integers 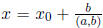 and
and
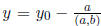 also satisfy the linear Diophantine equation
also satisfy the linear Diophantine equation
ax + by = c.
1.40. Question. If a, b, and c are integers and the linear Diophantine equation
ax+ by =
c has at least one integer solution, find a general expression for all the
integer solutions to
that equation. Prove your conjecture.
1.41. Theorem. Let a, b, c, be integers. Then the equation ax + by = c has a
solution
if and only if (a, b)|c. If 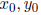 is a
solution, that is,
is a
solution, that is, 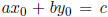 , then for every integer
k,
, then for every integer
k,
the integers 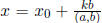 and
and
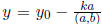 also satisfy the linear Diophantine equation
also satisfy the linear Diophantine equation
ax + by = c. Moreover, every solution to the linear Diophantine equation ax + by
= c is of
this form.
1.42. Theorem. If a and b are integers and k is a natural number, then gcd(ka,
kb) =
k gcd(a, b).
1.43. Formulate a definition. For natural numbers a and b, give a suitable
definition
for the least common multiple of a and b , denoted lcm (a, b). Construct and
compute some
examples.
1.44. Theorem. If a and b are natural numbers, then gcd(a, b) lcm(a, b) = ab.
1.45. Corollary. If a and b are natural numbers, then lcm(a, b) = ab if and only
if
gcd(a, b) = 1.
1.46. Big Picture Question: How are the ideas of greatest common divisor and
solutions
to linear Diophantine equations related?



