Introduction and Examples Of Matrix

DEFINITION: A matrix is defined as an ordered rectangular array of numbers. They can be
used to represent systems of linear equations, as will be explained below

Here are a couple of examples of different types of matrices:

Symmetric	Diagonal	Upper Triangular	Lower Triangular	Zero	Identity

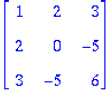And a fully expanded mxn matrix A, would look like this:

or in a more compact form: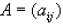

Matrix Addition and Subtraction

DEFINITION: Two matrices A and B can be added or subtracted if and only if their
dimensions are the same (i.e. both matrices have the identical amount of rows and columns.
Take:

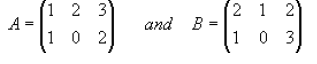
Addition
If A and B above are matrices of the same type then the sum is found by adding the
corresponding elements

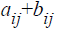
Here is an example of adding A and B together

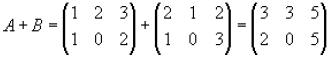
Subtraction
If A and B are matrices of the same type then the subtraction is found by subtracting the
corresponding elements

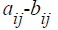
Here is an example of subtracting matrices

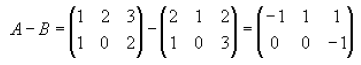
Now, try adding and subtracting your own matrices

Matrix Multiplication

DEFINITION: When the number of columns of the first matrix is the same as the number of
rows in the second matrix then matrix multiplication can be performed.

Here is an example of matrix multiplication for two 2x2 matrices

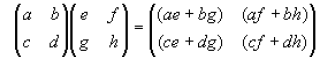
Here is an example of matrices multiplication for a 3x3 matrix

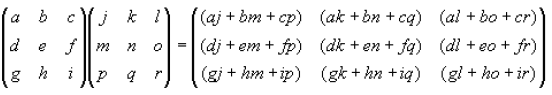
Now lets look at the nxn matrix case, Where A has dimensions mxn, B has dimensions nxp.
Then the product of A and B is the matrix C, which has dimensions mxp. The ij^th element of
matrix C is found by multiplying the entries of the i^th row of A with the corresponding entries
in the j^th column of B and summing the n terms. The elements of C are:

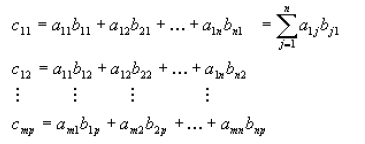
Note: That AxB is not the same as BxA
Now, try multiplying your own matrices

Transpose of Matrices

DEFINITION: The transpose of a matrix is found by exchanging rows for columns i.e.
Matrix A = (a_ij) and the transpose of A is:
A^T=(a_ji) where j is the column number and i is the row number of matrix A.

For example, The transpose of a matrix would be:

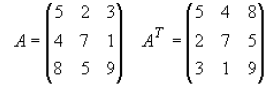
In the case of a square matrix (m=n), the transpose can be used to check if a matrix is
symmetric. For a symmetric matrix A = A^T

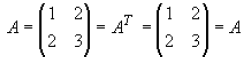
Now try an example

The Determinant of a Matrix

DEFINITION: Determinants play an important role in finding the inverse of a matrix
and also in solving systems of linear equations. In the following we assume we have a
square matrix (m=n). The determinant of a matrix A will be denoted by det(A) or |A|.
Firstly the determinant of a 2x2 and 3x3 matrix will be introduced then the nxn case will
be shown.

Determinant of a 2x2 matrix
Assuming A is an arbitrary 2x2 matrix A, where the elements are given by:

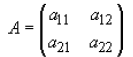
then the determinant of a this matrix is as follows:

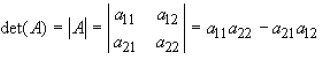
Now try an example of finding the determinant of a 2x2 matrix yourself

Determinant of a 3x3 matrix
The determinant of a 3x3 matrix is a little more tricky and is found as follows ( for this case assume
A is an arbitrary 3x3 matrix A, where the elements are given below)

then the determinant of a this matrix is as follows:

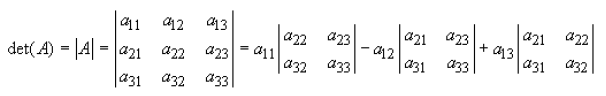
Now try an example of finding the determinant of a 3x3 matrix yourself

Determinant of a nxn matrix
For the general case, where A is an nxn matrix the determinant is given by:

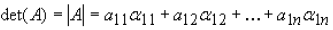
Where the coefficients 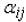are given by the relation

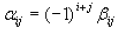
where 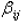is the determinant of the (n-1) x (n-1) matrix that is obtained by deleting row i and
column j. This coefficient 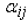is also called the cofactor of a_ij.

The Inverse of a Matrix

DEFINITION: Assuming we have a square matrix A, which is non-singular ( i.e. det(A)
does not equal zero ), then there exists an nxn matrix A^-1 which is called the inverse of A,
such that this property holds :

AA^-1= A^-1A = I where I is the identity matrix.

The inverse of a 2x2 matrix
Take for example a arbitury 2x2 Matrix A whose determinant (ad-bc) is not equal to zero

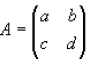
where a,b,c, d are numbers , The inverse is:

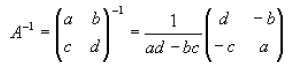
Now try finding the inverse of your own 2x2 matrices:

The inverse of a nxn matrix
The inverse of a general nxn matrix A can be found by using the following equation:

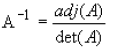
Where the adj(A) denotes the adjoint (or adjugate) of a matrix. It can be calculated by the following
method

•Given the nxn matrix A, define

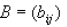
to be the matrix whose coefficients are found by taking the determinant of the (n-1) x (n-1)
matrix obtained by deleting the i^th row and j^th column of A. The terms of B (i.e. B = b_ij) are
known as the cofactors of A.
•And define the matrix C, where

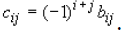
•The transpose of C (i.e C^T) is called the adjoint of matrix A.

Lastly to find the inverse of A divide the matrix C^T by the determinant of A to give its inverse.

Now test this method with finding the inverse of your own 3x3 matrices

Solving Systems of Equations using Matrices

DEFINITION: A system of linear equations is a set of equations with n equations and n
unknowns, is of the form of

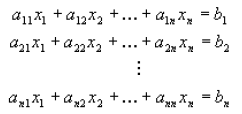
The unknowns are denoted by x₁,x₂,...x_n and the coefficients (a's and b's above) are
assumed to be given. In matrix form the system of equations above can be written as:

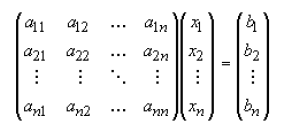
A simplified way of writing above is like this ; Ax = b

Now, try putting your own equations into matrix form by clicking here:

After looking at this we will now look at two methods used to solve matrices these are

•Inverse Matrix Method
•Cramer's Rule

Inverse Matrix Method

DEFINITION: The inverse matrix method uses the inverse of a matrix to help solve a
system of equations, such like the above Ax = b. By pre-multiplying both sides of this
equation by A^-1 gives:

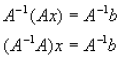
or alternatively this gives

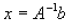
So by calculating the inverse of the matrix and multiplying this by the vector b we can
find the solution to the system of equations directly. And from earlier we found that the
inverse is given by

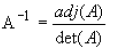
From the above it is clear that the existence of a solution depends on the value of the
determinant of A. There are three cases:

1. If the det(A) does not equal zero then solutions exist using
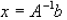
2. If the det(A) is zero and b=0 then the solution will be not be unique or does not
exist.
3. If the det(A) is zero and b=0 then the solution can be x = 0 but as in 2. is not unique
or does not exist.

Looking at two equations we might have that

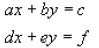
Written in matrix form would look like

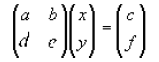
and by rearranging we would get that the solution would look like

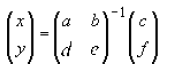
Now try solving your own two equations with two unknowns

Similarly for three simultaneous equations we would have:

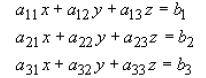
Written in matrix form would look like

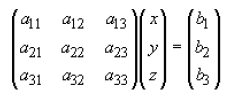
and by rearranging we would get that the solution would look like

Now try solving your own three equations with three unknowns

Cramer's Rule

DEFINITION: Cramer's rules uses a method of determinants to solve systems of
equations. Starting with equation below,

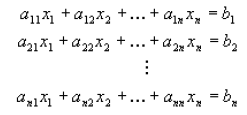
The first term x ₁ above can be found by replacing the first column of A by

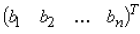. Doing this we obtain:

Similarly for the general case for solving x_r we replace the r^th column of A by
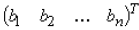and expand the determinant

This method of using determinants can be applied to solve systems of linear equations .
We will illustrate this for solving two simultaneous equations in x and y and three
equations with 3 unknowns x, y and z.

Two simultaneous equations in x and y

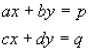
To solve use the following:

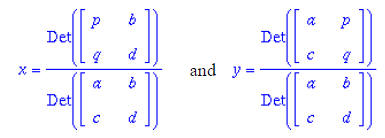
or simplified:

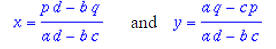
Now try solving two of your own equations

Three simultaneous equations in x, y and z

ax+by+cz = p
dx+ey+fz = q
gx+hy+iz = r

To solve use the following:

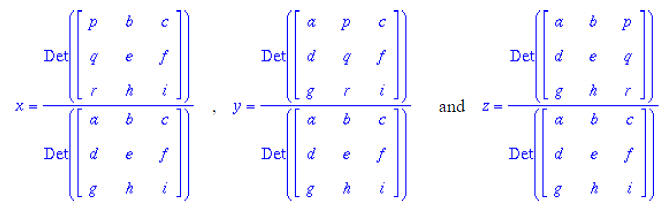
Now try solving your own three equations