There are occasions when it may be necessary to use two or
more functions in sequence, in the
sense that the output from one function is required as the input to another
function. Consider the
following scenario.
The Creative Candle Company produces spherical candles. The production
manager needs to determine the cost of producing a candle having a radius of
4.2 cm. The volume V of a candle is a function of its radius r:
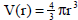 .
.
Because larger candles require more wax, the cost of producing a candle
depends upon its size. If V is the volume of the candle, then the production
cost
C (in dollars) is given by the function
C(V) = 0.0021V + 0.19 .
To determine the cost, the manager must first determine the volume, which is
V(4.2) ≈ 310.3 cubic centimeters . This value can now be used to obtain the cost
according to the second function. Since C(310.3) ≈ 0.842, the cost will be
approximately 84 cents per candle.
In the above scenario, notice how the output (volume) from the first function
was required as
an input for the second function. In order to determine the cost, the two
functions had to be used in
sequence: radius => volume => cost. This process is referred to as function
composition.
| Definition:
If f and g are two functions , then
the composition of f and g, written f o g , is defined as:
( f o g)(x) = f ( g(x)) .
The domain of f o g is {x: x is in the domain of g and g(x) is in the
domain of f}. That is, g must
be defined at x and f must be defined at the output g(x). |
To find a composition, notice that the functions are used
right to left. The function g is
evaluated at x first, yielding the output g(x). The value g (x) is then used as
an input to f, giving the
final result of f(g(x)).
A good way to visualize function composition is to imagine an assembly- line
process (see
Figure 1). Each function in the composition is only one step of the whole
process, performing its
specialized task and sending the "unfinished product" on to the next function
for further
processing.
Domain
of g |
Unfinished
product |
Final
result |
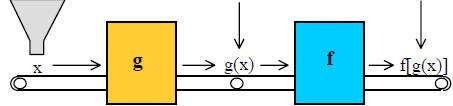 |
Figure 1
For problems 1–10, find (a) ( f o g)(2) , (b) (g o f )(2)
, (c) ( f o g)(x) , and (d) (g o f )(x) . Write your answers in
simplified form .
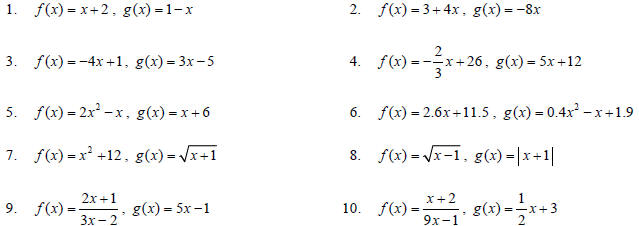
For problems 11–16, find (a) (f o g)(x), (b) (go f)(x),
(c) (f o f)(x), and (d) (go g)(x). Write your answers in simplified
form.
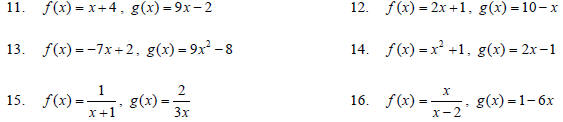
For problems 17–18, use the table definitions of H(t) and
r(t) shown below to find the indicated composition.

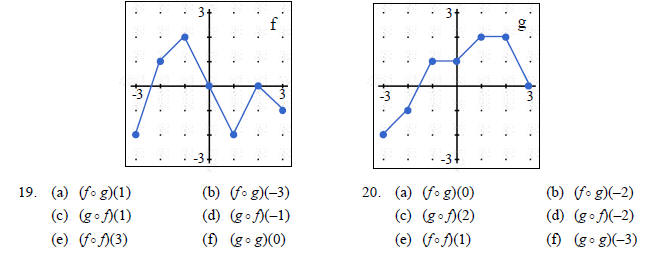
For problems 19–20, use the graphs of f (x) and g(x) shown
to find the indicated composition.
21. The temperature T (°F) of gas in a helium balloon is
increasing with time according to the function T = 4.3t + 56,
where the time t is measured in hours. The volume V ( cubic inches ) of the
balloon is a function of the temperature
of the gas inside, V = 0.28T. Find (V o T)(4) and explain what this value
represents in terms of the balloon .
22. The radius r (in meters) of a circular oil spill is growing over time (in
hours) according to the function 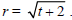
The area A of the oil slick is a function of the radius, A = π r2 . Find (Ao
r)(5) and explain what this value
represents in terms of the oil spill.
23. The Spinomatic company is planning a week long promotion in which washing
machines will be discounted by
15% off the retail price. In addition , customers who purchase a washing machine
during the first day of the
promotion will receive a special discount of $25. Let P(x) = 0.85x be the
discount function which gives the sale
price after the 15% discount, and let S(x) = x – 25 be the special discount
function which deducts $25 off of the
price x of the washing machine. Find (P o S)(x) and (S o P)(x) and explain the
meaning of each in terms of price
discounts. If you were a customer, which composition would you prefer ?
24. Suppose n(T) predicts the number of tropical storms each year in the
Caribbean, where T represents the average
temperature of the Atlantic ocean during June of that year, and I(n) gives an
estimate of the total cost of stormrelated
insurance claims based on the number of tropical storms. Explain what I o S
represents and how it might
be useful to insurance companies.
Answers
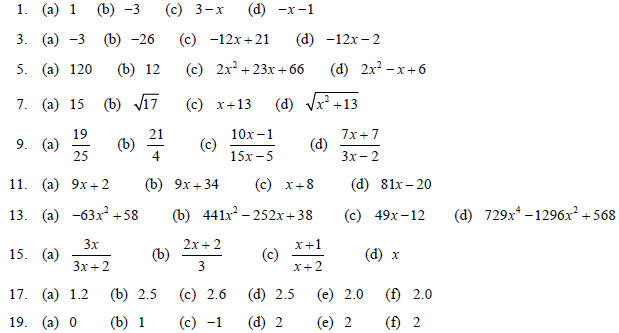
21. 20.496; After 4 hours, the volume of the balloon is
20.496 cubic inches.
23. (Po S)(x) = 0.85x - 21.25 , (S o P)(x) = 0.85x - 25 . With Po S , the 15%
discount is taken after the price is
reduced by $25. With S o P , the $25 deduction is taken after the price is
discounted by 15%. Since 0.85x - 25
will be less than 0.85x - 21.25 for any x, the better deal is to take the 15%
discount first.



