Welcome to the course! Much of today we’ll discuss
the administration of the course.
We will discuss the general description of the course, its
goals and objectives, the syllabus,
the textbook, assignments, quizzes, tests, course grade, and various sundry
items.
Systems of linear equations . After discussing the course in general,
we’ll move on the
subject matter. We’re starting out with something you already know, systems of
linear
equations. You’ve looked at these before in various algebra classes , so this is
really a summary .
There are many ways to solve such a system, but we’ll concentrate on a
systematic method
called elimination .
We’ll begin by looking at the the method of elimination as the ancient Chinese
did it.
It’s a standard algorithm that’s been rediscovered over and over. For this
algorithm, a
matrix of numbers is formed from the system of linear equations . For the time
being, the
word “matrix” just means a rectangular array of numbers. As we add operations on
matrices
(“matrices” is the plural of “matrix”), the concept of matrix will mean more
than just a
rectangular array.
Once the matrix of numbers is formed from the system of linear equations , we
will Then
it’s converted into what ’s called “echelon form,” and converted further into
what’s sometimes
called “ reduced echelon form.” From that, the solution can be read directly off
the resulting
matrix.
When there are the same number of equations as there are unknowns, frequently
the
system of equations has exactly one solution. But sometimes such a system has no
solutions,
and sometimes it has infinitely many solutions.
Matlab. We’ll use Matlab to illustrate topics in linear algebra. It’s available
in the
computer lab.
Our text discusses Matlab in Chapter 12. Read the first
couple of sections for an introduction.
Below is a short Matlab session to solve the following
system of linear equations.
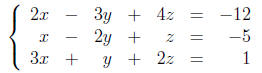
In the session, a matrix A is created that holds the
coefficients , and a column vector b holds
the constants. The solution is computed with the instruction x = A\b which says
the solution
is (x, y, z) = (1, 2,−2).
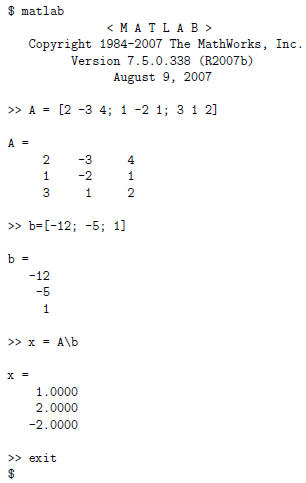
Due Wednesday. Exercises from section 1.1, page 8,
numbers 1–4, 13–14, 21–22, 23, and
T4.
Read for Wednesday sections 1.1 on linear systems and 1.2 on matrices.
Due Friday. Exercises from section 1.2: 1–2, 4–7 parts a–d each, 8, 9, T1,
T5a.