An Introduction to Algebra and Simplifying Algebraic Expressions
An Introduction to Algebra and Simplifying Algebraic
Expressions
Objective: To use the order of
operations and distributive
property to simplify expressions. |
Introduction
 In arithmetic , we
perform mathematical In arithmetic , we
perform mathematical
operations with specific numbers. In
algebra, we perform these same basic
operations with numbers and variables,
which are letters that stand for
unknown quantities . |
| Definitions  variable – a symbol, usually a letter, that
variable – a symbol, usually a letter, that
represents one or more numbers
 algebraic expression – a math phrase with algebraic expression – a math phrase with
numbers, variables, and operation symbols
 evaluate – substitute and simplify evaluate – substitute and simplify
|
The following are some basic mathematical
properties that we will apply: Commutative: a + b = b + a; ab = ba
Commutative: a + b = b + a; ab = ba
 Associative: (a + b) + c = a + (b + c); Associative: (a + b) + c = a + (b + c);
(ab)c =a(bc)
 Distributive: a(b + c) = ab +ac Distributive: a(b + c) = ab +ac
 a + 0 = a a + 0 = a
 a(0) = 0 a(0) = 0
 a + (-a) = 0 a + (-a) = 0
 a(1) = a a(1) = a
|
| Order of Operations, pg. 202
1. Grouping symbols (parentheses,
brackets , fraction bar)
2. Exponents
3. Multiply and divide in order from left
to right.
4. Add and subtract in order from left to
right. |
P.E.M.D.A.S.  Please Excuse My Dear Aunt Sally!
Please Excuse My Dear Aunt Sally!
1. P – parentheses (any grouping symbols)
2. E – exponents
3. M/D – multiply/divide (left to right)
4. A/S – add/subtract (left to right)
|
Simplify using the Order of
Operations.
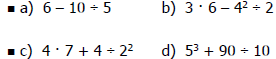 |
Your Turn: Simplify using the
Order of Operations.
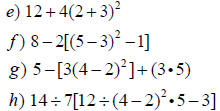 |
| Evaluating an Expression
 To evaluate 2x - y when x = 5 and y = -3, To evaluate 2x - y when x = 5 and y = -3,
replace the variables with their values in
parentheses and simplify.
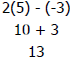 |
Evaluate if x = 2.
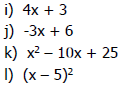 |
| Simplifying Algebraic Expressions
 term – a number, a variable, or a term – a number, a variable, or a
product of a number & variable(s)
 constant – a number that does not constant – a number that does not
change in value
 coefficient – a numerical factor of a coefficient – a numerical factor of a
term (the number in front of a variable)
 like terms – exactly the same variable like terms – exactly the same variable
and power |
An explanation  Terms are always separated by a plus
Terms are always separated by a plus
(or minus) sign. For example, the
expression 2x - 3y has two terms , 2x
and -3y. In this expression, 2 and -3
are constants, x and y are variables
with 2 being the coefficient of x and -3
the coefficient of y.
 The expression 2x +3y -5 has 3 terms. The expression 2x +3y -5 has 3 terms.
|
Example: Simplify each expression by
combining like terms .
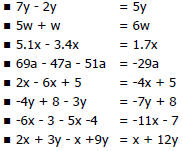 |
Distributive Property
 If an algebraic expression that appears If an algebraic expression that appears
in parentheses cannot be simplified,
then multiply each term inside the
parentheses by the factor preceding the
parentheses . Then combine like terms. |
| Distributive Property Practice
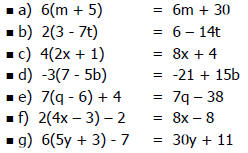 |
Parentheses  If an
expression inside parentheses is If an
expression inside parentheses is
preceded by a “+” sign, then remove
the parentheses by simply dropping
them. For example:
3x + (4y + z) = 3x + 4y + z. |
| Parentheses  If an
expression in parentheses is If an
expression in parentheses is
preceded by a “-” sign then it is removed
by changing the sign of each term inside
the parentheses and dropping the
parentheses. For example,
3x – (4y – z) = 3x – 4y + z.
(This is like distributing a negative one .)
|
Simplify
 |
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
May 2nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
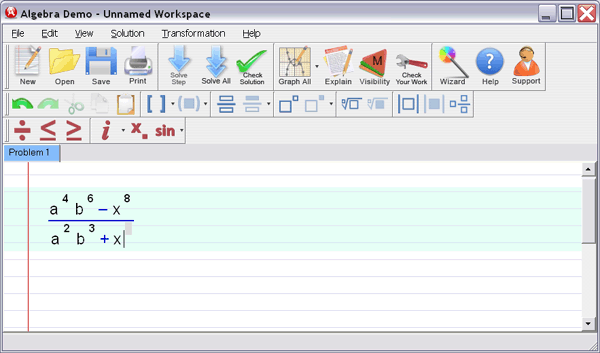
Step 2 :
Let Algebra Helper solve it:
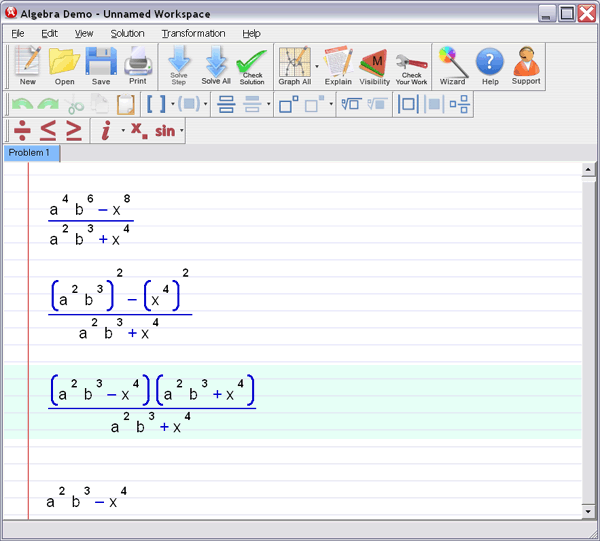
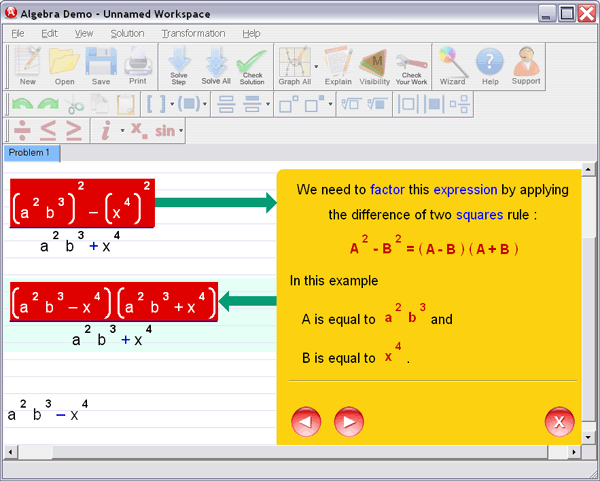
Step 3 : Ask for an explanation for the steps you don't understand:
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



