Big example, superposition, and Frequency Response
[1] Example. 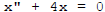
PLEASE KNOW the solution to the homogeneous harmonic oscillator
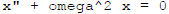 are sinusoids of circular frequency omega !
are sinusoids of circular frequency omega !
Here, 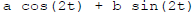 .
.
In the real example I drive it: 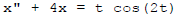 .
.
The complex equation is 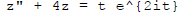 .
.
If it weren't for the t we could try to apply ERF:
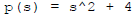 ,
,
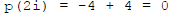 , though, so it doesn't apply; we do have
the
, though, so it doesn't apply; we do have
the
resonance
response formula , which gives 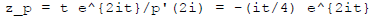
so 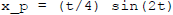 .
.
But there is a t there. We should then use "Variation of Parameters":
Look for solutions of the form
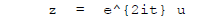 for u an Unknown
function .
for u an Unknown
function .
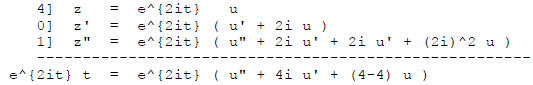
so 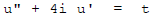
Reduction of order : 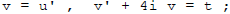
Use undetermined coefficients : 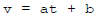
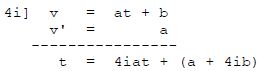
so 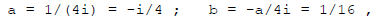
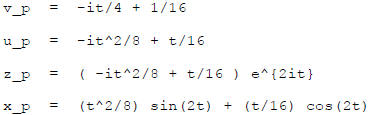
The general solution is then
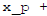 the homogeneous solution.
the homogeneous solution.
[3] Superposition: putting special cases together .
Suppose a bank is giving I percent per year interest:

Suppose that I open TWO bank accounts and proceed to save at rates
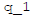
(t)
and 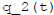 in them.
in them.
Is this any different than opening ONE bank account and saving at the
rate
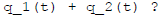
Say the solutions with savings rates 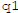 and
and
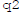 are
are 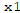 and
and
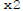 .
.
Is 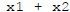 a solution with savings rate
a solution with savings rate
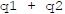 ?
?
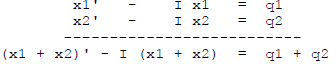
since differentiation respects sums (and multiplying by I
does too).
In general if 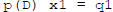 and
and
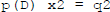
then 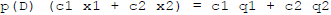
In fact this is true for nonconstant coefficient linear equations too.
It is the essence of linearity, and it's the most general form of the
superposition principle.
It lets you break up the input signal into constituent parts, solve for
them separately, and then put the results back together. This is why it isn't
so
bad that we spent all that time studying very special input signals.
One example is when 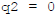 : then
: then
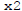 is a solution to the
is a solution to the
homogeneous
equation, and we find again that adding such a function to a solution of
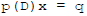 gives another solution.
gives another solution.
Our work has shown a general result:
Theorem: If q(t) is any linear combination of products of polynomials
and exponential functions, then all solutions to
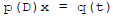 are
are
again
linear combinations of products of polynomials and exponential
functions.
Here we mean *complex* linear combinations and *complex* exponentials,
so for example 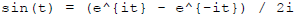 is a possible signal
is a possible signal
or solution.
[4] Frequency response
Polar form of a complex number : 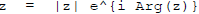
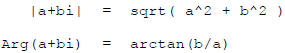
Frequency response is about the amplitude and phase lag of
a sinusoidal
(steady state) response of a system to a sinusoidal signal of some
frequency.
It is based on the following method of finding a sinusoidal system
response in "polar" (amplitude/phase lag) form:
Example:

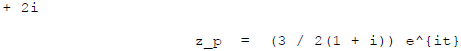
Now write 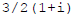 in polar
form . Do the denominator first :
in polar
form . Do the denominator first :
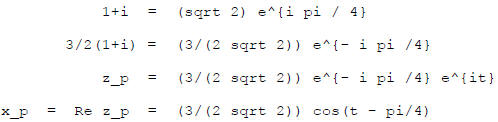
Lesson: if 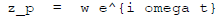
then
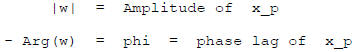
Suppose now that I let the input frequency be anything:
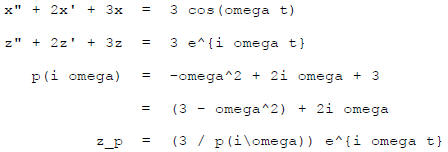
So the amplitude of the sinusoidal response is
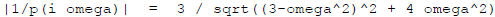
This takes value 1 at omega = 0 , and when omega is large
it
falls off like 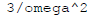 . In this case, it reaches a
modest
. In this case, it reaches a
modest
"near resonance" peak at omega = 1 .
The phase lag is 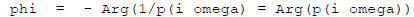
There's no particular advantage in writing out a more explicit formula
for this.
Good luck!



