The following are fundamental functions whose stated properties and graphs
you must
know.
1 . The Constant Function
y = f(x) = c
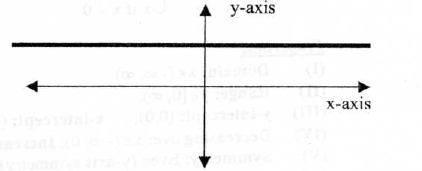
Properties :
(I) Domain :
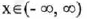
(II) Range:
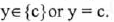
(III) y- intercept : (0, c)
x- intercept : None except for y = f(x) = 0 (In this case the x-axis is the
graph)
(IV) Constant over
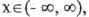that is, always constant
(V) Symmetry: Even (y-axis symmetry)
(VI) End Behavior:
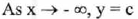
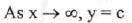
(VII) No asymptote .
2.The Identity Function
y = f(x) = x
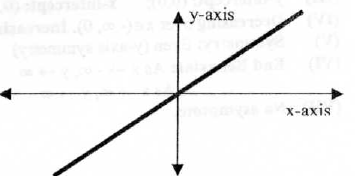
Properties :
(I) Domain :
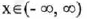
(II) Range:
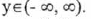
(III) y-intercept: (0,0) ; x-intercept : (0,0)
(IV) Increasing over
,
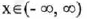that is, always increasing
(V) Symmetry: Odd (origin symmetry)
(VI) End Behavior :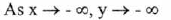
(VII) No asymptote.
3.The Absolute Value Function
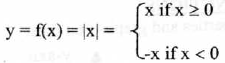
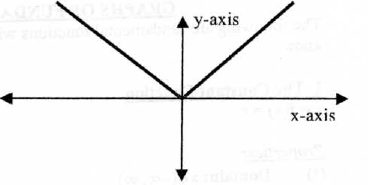
Properties:
(I) Domain :
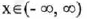
(11) Range :
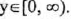
(III) y-intercept : (0,0) ; x-intercept : (0,0)
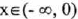(IV) Decreasing over
.
Increasing over
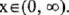
(V) Symmetry: Even (y-axis symmetry)
(VI) End Behavior: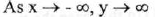
(VII) No asymptote.
4. The Square Function
y=f(x)=x^2
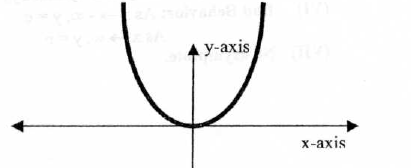
Properties:
(I) Domain :
,
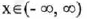(II) Range :
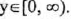
(III) y-intercept : (0,0) ; x-intercept : (0,0)
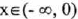(IV) Decreasing over
.
Increasing over
.
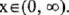(V) Symmetry: Even (y-axis symmetry)
(VI) End Behavior:
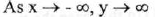
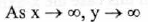
(VII) No asymptote.
5. The Cube Function
y = f(x) = x^3
Properties :
(I) Domain:
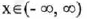
(II) Range: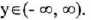
(III) y-intercept : (0,0); x-intercept: (0,0)
(IV) Increasing over
;
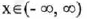that is, always increasing
(V) Symmetry: Odd (origin symmetry)
(VI) End Behavior:
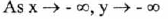
(VII) No asymptote.
6. The Square - Root Function
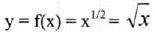
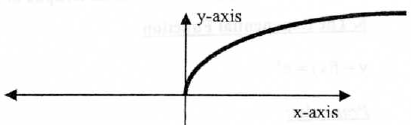
Properties:
(I) Domain:
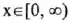
(II) Range:
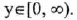
(III) y-intercept: (0,0) ; x-intercept: (0,0)
(IV) Increasing over
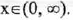
(V) Symmetry: None
(VI) End Behavior :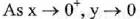
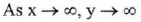
(VII) No asymptote.
7.The Reciprocal Function
y = f(x) = 1/x
Properties:
(I) Domain :
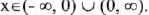That is, all real numbers except x = 0.
(II) Range:
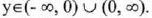That is, all real numbers except y = 0.
(I1I) y-intercept: None; x-intercept: None
(IV) Decreasing over
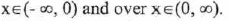
(V) Symmetry : Odd (origin symmetry)
(VI) End Behavior :
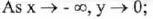
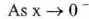(approaches
0 from the left),
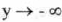
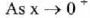(approaches
0 from the right),
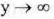
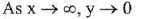
(VII) Vertical asymptote: x = 0 (y-axis) ; Horizontal asymptote : y = 0 (x-axis)
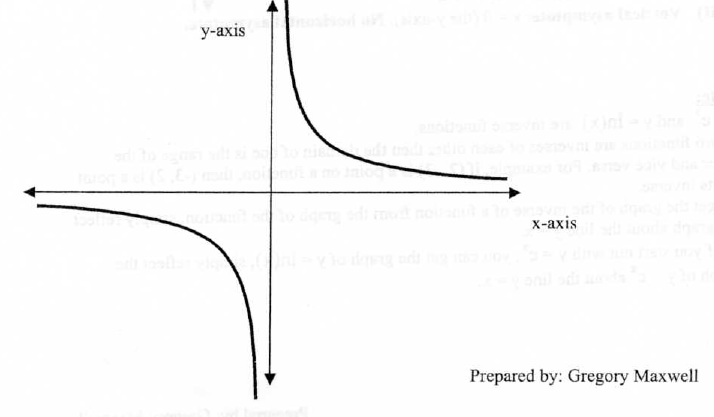
8. The Exponential Function
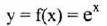
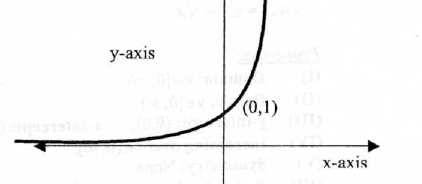
Properties:
(I) Domain:
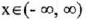
(1I) Range:
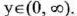
(III) y-intercept : (0,1) ; x-intercept : None
(IV) Increasing over
;
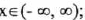that is, always increasing
(V) Symmetry: None
(VI) End Behavior :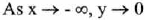
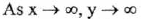
(VII) Horizontal asymptote : y = 0 (the x-axis) . No vertical asymptote.
9. The Natural Logarithm Function
y = f(x) = ln(x)
Properties:
(I) Domain :
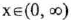
(II) Range :
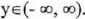
(III) y-intercept: None; x-intercept : (1,0)
(IV) Increasing over
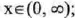that is, always increasing
(V) Symmetry: None
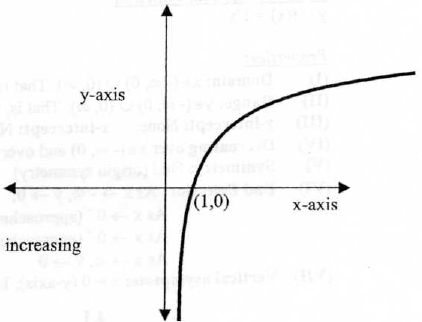
(VI) End Behavior:
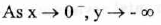
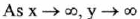
(VII) Vertical asymptote : x = 0 (the y-axis) . No horizontal asymptote.
Note:
y = ex and y = ln(x) are inverse functions.
If two functions are inverses of each other then the domain of one is the range
of the
other and vice versa . For example, if (2, -3) is a point on a function, then
(-3, 2) is a point
on its inverse.
To get the graph of the inverse of a function from the graph of the function,
simply reflect
the graph about the line y = x.
So if you start out with y = eX , you can get the graph of y = ln(x), simply
reflect the
graph of y = ex about the line y = x .
