Table 14: Linear and Angular Velocity
Table 15: Units relations
| 1 mile = 5280 feet |
1 feet = 12 inches |
| 1 hour = 60 mins |
1 min = 60 sec |
Table 16: Radian Formula . s: length of arc, r: radius, P:
perimeter of sector, A: area of sector,
θ: angle in radian
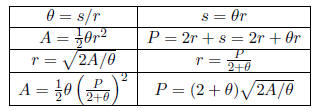
5 Test 5 Chapter 8.3, 8.4, 8.5, 8.7, 9.1, 9.2
5.1 8.3 Graph of Sine and Cosine
Table 17: Graph of Sine and Cosine
| |
Asin(Bx + C) + D |
Acos(Bx + C) + D |
| Domain |
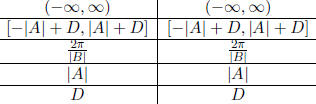 |
| Range |
| Period |
| Amplitude |
| Median |
Phase of Shift
(Starting Point) |
 |
 |
Table 18: Graph of Tan and Cot
| |
Atan(Bx + C) + D |
Acot(Bx + C) + D |
| Domain |
{x|Bx + C ≠ k(π /2), k is any odd number } |
{x|Bx + C ≠ kπ , k is any even number} |
| Range |
(−∞,∞) |
(−∞,∞) |
| Period |
π/|B| |
π/|B| |
Table 19: Graph of Sec and Csc
| |
Asec(Bx + C) + D |
Acsc(Bx + C) + D |
| Domain |
{x|Bx + C ≠ k( π/2), k is any odd number} |
{x|Bx + C ≠ kπ , k is any even number} |
| Range |
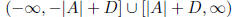 |
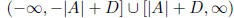 |
| Period |
2π /|B| |
2π /|B| |
Table 20: Chart of Special Angle
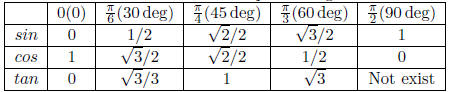
Table 21: Maximum Points
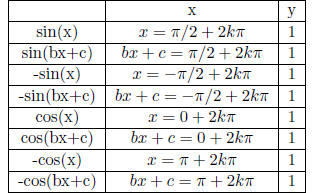
Table 22: Minimum Points
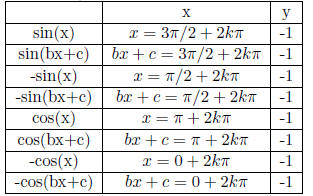
Table 23: Useful formula
6 Test 6-Chapter 9.4 9.5 10.1
Contents: Inverse Trig Function , Law of sine and cosine
1. Domain and Range (table (??)):
Table 24: Inverse Function
| Function |
arcsin(x) |
arccos(x) |
arctan(x) |
| Domain |
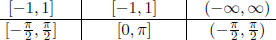 |
| Range |
Quadrant
|
1st and
4th |
1st and
2nd |
1st and 4th |
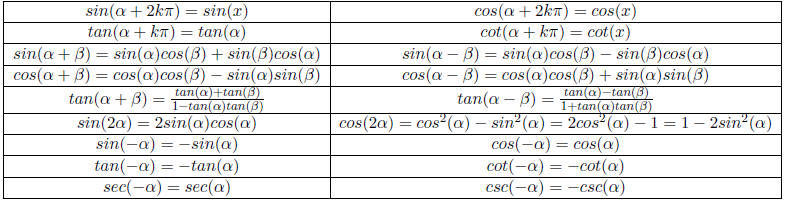
Table 25: Useful Properties
| Properties |
Examples |
 |
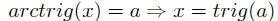 |
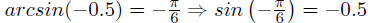 |
trig(a) = x doesn’t necessary implies
a = arctrig(x) |
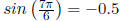
but 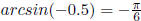 |
| trig(arctrig(x)) = x |
sin(arcsin(x)) = x |
| arctrig(trig(x)) = x, iff x ∈
the range of arctrig |
arccos(cos(x)) = x, iff x ∈ [0, π] |
if 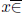 the range of arctrig,
the range of arctrig,
arctrig(trig(x)) = α , where α ∈ the range
such that trig(x) = trig(α ). |
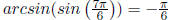
because 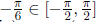
and 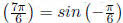 |
Example 6.1 Find the exact value of
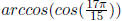 .
.
Analysis: let
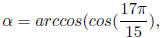
then by the definition of the range of arccos, α ∈ [0, π]. And
by taking cos at both side, we have
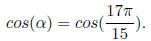
We know, if |trig(α )| = |trig( β )|, then ref( α ) = ref( β).
Hence we have
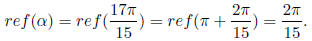
since 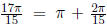 is in the 3rd quadrant, and cos in 3rd
quadrant is negative , it implies
is in the 3rd quadrant, and cos in 3rd
quadrant is negative , it implies
cos( α ) < 0. If combined with the fact that α can either be in the
1st or 2nd quadrant, we deduce
that α must be in the 2nd quad. In summary α is an angle in 2nd
quadrant with reference angle
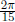 . Hence it must be
. Hence it must be
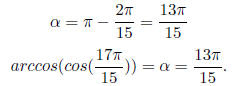
Example 6.2 Find the exact value of
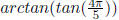 .
.
Solution : Let 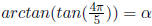
=>
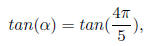
where 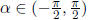
or, α in 1st or 4th quadrant.
1. Reference angle
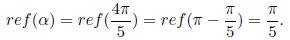
Moreover, 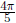 is in the
2nd quadrant, where tan value is negative . Hence
is in the
2nd quadrant, where tan value is negative . Hence
2. α is in the 4th quad where tan value is also negative .
3. So
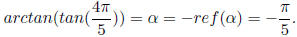
Example 6.3 Find the exact value of
sin(2arctan(−3/4))
Solution:
Let arctan(−3/4) = α, then
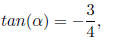
where 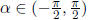 or, α is
either in the 1st or 4th quadrants.
or, α is
either in the 1st or 4th quadrants.
We can narrow the range of α, by observing that tan( α ) < 0, which
implies α can not be in the
first quadrant but in the 4th quadrant.
Since,
sin(2arctan(−3/4)) = sin(2 ) = 2sin(α )cos( α),
we need to find out sin( α ) and cos(α ), of which we know α in
4th quadrant, and tan(α ) = −3/4.
By using the assistant right triangle in the 4th quadrant, we have
sin( α ) = −3/5,
cos(α ) = 4/5,
sin(2α ) = 2(−3/5)(4/5).
6.1 Law of Sine and Cosine
Table 26: Law of Sine and Cosine
| Name |
Rule |
Usage |
| Law of Sine |
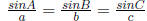 |
two angles + one side |
| Law of Cosine |
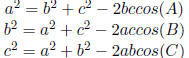 |
two sides + one anlge |
| Law of Cosine |
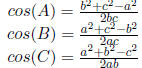 |
three sides |
Table 27: Useful Knowledge
| Sum of the 3 angles of a triangle is π or
180deg. |
Sum of the n angles in a regular n-gon is (n − 2)π
.
That means each angle is 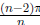 |
Largest angle opposites to largest side, smallest
angle opposites to smallest side. If A > B > C, then a > b > c. |



