Graphing and Circles

Overview

• Section 2.1 in the textbook:
– Cartesian Plane
– Distance & Midpoint Formulas
– Graphing Equations
– Intercepts
– Circles

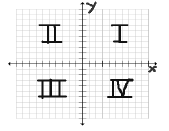
Cartesian Plane

• The Cartesian Plane consists of two number
lines – one horizontal and one vertical
– The point of intersection of the two lines is known as
the origin and has coordinates (0, 0)
– A coordinate (x, y) consists of two numbers :
  • x represents the horizontal (left to right) direction from the
origin
  • y represents the vertical (top to bottom) from the origin
• We plot points by starting at the origin and then
using the x and y parts of the point

– Split into four sections called quadrants
based on the sign of x and y of the coordinate
(x, y)

Cartesian Plane (Example)

Ex 1: Plot the following points on the
Cartesian Plane and tell the quadrant in
which each lies: (-5, 3), (0,2), (1, 1),
(-4, -4), (-3, 0), (2, -1)

Distance & Midpoint Formulas

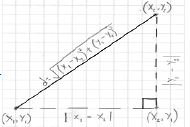
Distance Formula

• Sometimes we want to know the distance between two
points on a graph that may not necessarily lie on a
straight line
• Use the Pythagorean
Theorem
• From this, we get the
distance formula for
any two points
(x₁, y₁) and (x₂, y₂):

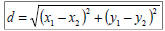
Midpoint Formula

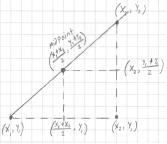
• Sometimes we need to know the midpoint of the line
segment between (x₁, y₁) and (x₂, y₂)
• Thus, the midpoint of the
line segment connecting
(x₁, y₁) and (x₂, y₂) is:

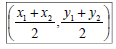
Distance & Midpoint Formulas
(Example)

Ex 2: Find the distance and midpoint of
(-6, 2) and (-1, -1). For the distance, give
both the exact and approximate answers.

Ex 3: Find the distance and midpoint of
(4, 5) and (2, -6). For the distance, give
both the exact and approximate answers.

Graphing Equations

• Given an equation, we can pick values for
one of the variables and solve for the other
– Ex: Given y = -x⁴ -> when x = -2, y = -16
 • Thus, (-2, -16) lies on the graph of y = -x⁴
• By repeating the process a few times , we
obtain a graph of the equation
– Usually 3 to 4 points are satisfactory
– Pick both positive and negative values

Graphing Equations (Example)

Ex 4: Graph using a table of values:
y = |x – 3| + 1

Ex 5: Graph using a table of values:

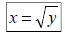
Intercepts

• x-intercept: where the graph of an
equation crosses the x-axis
–Written in coordinate form as (x, 0)
– To find, set y = 0, and solve for x :
  • May entail solving a linear or quadratic equation
• y-intercept: where the graph of an
equation crosses the y-axis
–Written in coordinate form as (0, y)
– To find, set x = 0, and solve for y

Intercepts (Example)

Ex 6: Find the x and y intercepts of

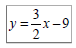
Ex 7: Find the x and y intercepts of

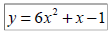
Circles

Standard Equation of a Circle

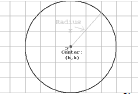
• Circle: the set of all points r units away, where r
is the radius, from a point (h, k) called the
center
• Given the radius and the center, we can
construct the standard equation of a circle:

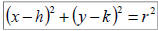
where:
(h, k) is the center
r is the radius

Standard Equation of a Circle
(Example)

Ex 8: Find the standard equation of a circle
with center (-2, 1) and contains the point
(0, 3)

Ex 9: Find the standard equation of a circle
with a diameter of (-1, -2) and (5, -6)

General Equation of a Circle

• There is another commonly used form of
the equation of a circle
• Ex: Start with the standard equation
(x – 3)^2 + (y + 2)^2 = 16
– Square the binomials :
x^2 – 6x + 9 + y^2 + 4y + 4 = 16
– Collect like terms :
x^2 – 6x + y^2 + 4y + 13 = 16
– Set the right side to 0 and rearrange the left:
x^2 + y^2 – 6x + 4y – 3 = 0
– This last equation can be written in the form
x^2 + y^2 + Ax + By + C = 0 (A, B, and C are
constants) and is known as the general
equation of a circle
  • Notice that the right side of the general equation
is set to 0
• Complete the square to convert the
general equation to the standard equation
– Complete the square on x
– Complete the square on y

General Equation of a Circle
(Example)

Ex 10: Find the center and radius of
x^2 + y^2 – 4x + y – 7 = 0

Summary

• After studying these slides, you should know how to do
the following:
– Graph points on a Cartesian Plane and be able to identify the
quadrant in which it lies
– Apply the distance and midpoint formulas
– Graph an equation by picking points
– Identify the intercepts of an equation
– Extract the center and radius of a circle from either the standard
or general equations
– Construct equations of circles
• Additional Practice
– See the list of suggested problems for 2.1
• Next lesson
– Introduction to Functions (Section 2.2)