Outline
Chaos:
Chapter 10
Definitions
Aside: Decimal expansion of Rational Numbers
Summary
Definition of Chaos
Definition
A dynamical system F is chaotic if
Periodic points of F are dense
F is transitive
F depends sensitively on initial
conditions |
We will define and then examine each of these conditions
and
verify they hold for the shift map on sequence space.
Density of Periodic Points
Definition
A subset D of a metric space, (X, dX ) is dense if there is a point
of D in every open ball. |
An statement is equivalent to : For every point x∈X there
is a
sequence of points dn ∈ D which converges to x.
Proof of Density of Q
Recall that a decimal number , i.e. real number in R is the
decimal expansion of a quotient of integers ( rational number
from Q) if and only if the decimal expansion is eventially
periodic.
Proof: If the eventual period is m, then 10mx - x is a finite
decimal (hence a quotient of integers) and so is
)
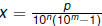Density of Rational Numbers
Proof: Viewing the real numbers as (equivalence classes,
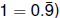decimal expansions, we need to find a
rational number
which is ε > 0 close. Choose a positive integer N with
.
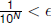Truncating the decimal expansion of x after the N decimal
place (or repeating zeroes ) gives a finite decimal expansion
which is the decimal expansion of a rational number.
Proof: Density of Periodic Points in ∑
Proof: In sequence space, ∑, given a sequence s and the
radius, ε of an open ball at s, choose an integer n with
.
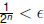Take the initial n + 1 terms of the sequence s and define a
periodic sequence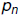 
which begins with these n + 1 terms and
then repeats them periodically. By the proximity theorem
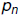is
distance less than ε from s. Note also, by the proximity
theorem, 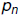converges to s.
Transitivity
Definition
A dynamical system F is transitive if for every pair of points x, y
and any ε > 0 there is a third point z with d[x, z] < ε and with
the orbit of z intersecting the ball of radius ε at y, that is, the
orbit of z passes at distance less than ε from y. |
A sequence s which embeds all finite sequences has an
orbit
which is dense. To construct such an s, enumerate all the finite
sequences of symbols ,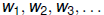 
and concatenate:
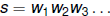
Sensitivity on Initial Conditions
Definition
A dynamical system F depends sensitively on initial conditions
if there is a number β > 0 such that for any x and any ε > 0
there is a y ε-close to x, i.e. d[y, x] < ε, and an integer k such
that d[Fk (x), Fk (y)] > β. |
Proof: Sensitivity of shift map
on Initial Conditions
For the shift map 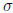, select β = 1. As usual, given a
sequence s
and ε > 0, choose an integer n with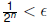 
.
Suppose T ∈∑ satisfies d[s, t] < 1/2n but t ≠ s. Then, by
proximity,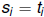
for i = 0, 1, . . . n and there is
an integer k > 0
with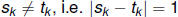 
. Then:
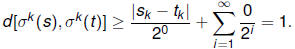
This completes the demonstration of sensitivity of shift
map
on initial conditions.
Summary of Chaos
A chaotic map possesses three properties :
Indecomposability: A transitive system cannot be
decomposed into two subsystems that do not interact.
Unpredictability: Sensitive dependence on initial conditions
Regularity: Periodic points are dense
