Tutoring Notes for Preliminaries

Chapter 1, entitled Preliminaries , is a review of pre-calculus topics. There is very
little in Chapter 1 that we will actually lecture on in class; students are required to review
it on their own by reading Sections 1.1, 1.2, 1.5, as well as handout materials on solving
inequalities and sign /direction/concavity of functions. Section 1.6 is the only section that
will be taught in class.

There are several homework assignments that cover all of Chapter 1 for students to work
on during the first two weeks of the semester. Our aim is to sharpen/refresh the students'
knowledge of pre-calculus topics and to reinforce the message to students that failing to
review this material adequately will hurt their performance in the course. Be on the lookout
for students in 10A who are having difficulty with this review and reiterate to them the
importance of having this material at their fingertips.

Many of the difficulties students have in this chapter are similar to those in 5A so I will
refer you back to the math 5A tutoring notes (see below).

A. Sections 1.1,1.2, & 1.5.

• The math 5A tutoring notes for Chapters 1 and 2 should guide you with most questions
10A students have here.

• Some students have a hard time recalling their trig. Since they probably used calcu-
lators in high school, they don't know some of the basic trig values that they must
memorize for 10A. Remind them that a review of basic trig at this point will help them
throughout the course.

• The only trig identity that students have to memorize in this course is sin²θ+cos²θ = 1.
They should also know:

- The trig values for sin , cos and tan for the angles 0, 30, 45, 60, 90, 180, 270 and
360 degrees (the so called "π/2, π/3, π/4 and π/6" families).
- How to find the angle when the sine, cosine, etc., of the angle is given.
- How to convert from radians to degrees and back.
- The basic relationships between the six trig functions such as sec 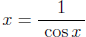, etc...
- American students learn a word to help memorize the trig ratios: SOHCAHTOA.
It reminds them that the ratios for a right triangle are

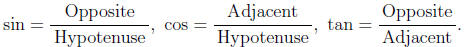
- Some students find trig equations hard . To be consistent we always ask for answers
in the interval [0; 2π]. For an equation like sin 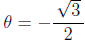you might want to say
something like: " What are the values of µ in the interval [0; 2π] whose sin is
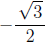?" After students have studied Section 1.6, they can also approach these
equations using inverse trig functions.

B. Polynomial and Rational Inequalities.

• Look at the Chapter 1 tutoring notes for math 5A (Section 1.7) for the algorithm we
use to solve polynomial and rational inequalities. We will use the same method in
math 10A.

• The difficulties students have here are also the same as those listed in the math 5A
Section 1.7 tutoring notes.

C. Sign, Direction and Concavity of Functions.

• We define (without reference to the derivative) what it means for a function to be:

- positive/ negative on an interval
- increasing/decreasing on an interval
- concave up/concave down on an interval

• At this point we mainly use the graphical definitions of the above terms .

• As in math 5A remind students that for checking increasing/decreasing we look at the
graph from left to right
(not right to left)

D. Inverse Functions and Logarithms (Section 1.6).

• Students can identify 1-1 functions using the horizontal line test ; we don't insist on
more formal reasoning. (Students generally feel more comfortable with graphical ex-
planations than with abstract algebraic expressions. This is one thing you should bear
in mind when tutoring.) They also need to be able to ¯nd the inverse of a function
like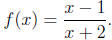. Remind them to go through the following three steps rigorously :

- Rewrite the expression into
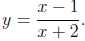
- Solve for x in the resulting equation, by regarding y as a constant.
- You will get something like 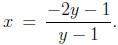In this expression, replace x with
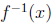and y with x.

As you will learn, some students will have trouble with the algebra involved in the
second step.
For some kinds of inverse function problems, it is helpful to remind the students that

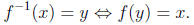
• The only inverse trig functions we introduce in this course are sin^-1 x and tan^-1 x.
Such questions as finding the value of tan 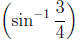require drawing an illustrating
triangle. The unit circle method is frequently used, and the graphs of sin x and tan x
are sometimes very useful.

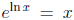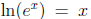• Of course we use the identities and to solve exponential and
rational equations however students usually say something like \take ln of both sides"
when they are solving exponential equations and \raise both sides to the e" when they
are solving a log equation. (This last phrase is wrong, of course, but when students
say it they are generally doing the right thing. They will also understand if you use
the correct phrase, \exponentiate both side".)

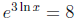• is an important example. Students frequently say that 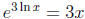; some of
them make this kind of error repeatedly through the semester.

• In an example like 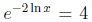students forget to notice that x = -1/2 is not a valid
solution.

• 4 ln x = -8 is also an important example. Students often claim that an equation like
this has no solutions , since \natural log can't be negative". What they're doing is
confusing the input and output of ln x.

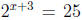• is another basic example. Students tend to either start by taking ln on
both sides of the equation | of course they could succeed if doing it correctly | or
simply get lost. It is a good point to tell them to \choose the right base when taking
logarithm".

• ln(2x - 1) - 2 ln x = 0 is yet another very important example since students often
exponentiate incorrectly as follows: 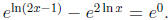In can be hard to convince
some students that this is wrong. To do so, start with a simple equation like 2+3 = 5
and point out that 2² + 2³ ≠ 2⁵.

• Solving exponential and logarithmic inequalities is not covered in the text. However
these come up, of course, when students are analyzing derivatives involving e^x and ln x
later on in the course, so we teach them now. Usually students find these difficult at
first. We need to remind them to use the number line (0;∞) when ln x is present.

• Two examples of inequalities:

1. xe^x + 2e^x > 0 is a relatively simple inequality. Students must remember what
they learned earlier in the section about solving inequalities and remember that
e^x > 0 for all x.

2. x - 2x ln x > 0 is harder for students. First they have to notice that since the
domain of ln x is (0;+∞), their number line analysis takes place only on the
positive real line. They also have to figure out how to find \test points" in the
intervals 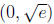and 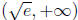. They're used to choosing integer test points, of
course, which don't work well here without a calculator . Point out that the best
kind of test point is a power of e . For instance, for the interval 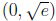, they can
choose the test point 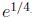-or any point of the form 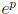, where p <1/2. Similarly
for 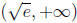they can choose e, e², etc., or any power of e higher than 1/2.