4.3. A Short Quiz to Test Yourself
Now try a few for yourselves. After you solve the problem , click on the green
link
of your choice to get immediate feedback to your choice.
Quiz Solve each of the following systems using any method you choose.
1.
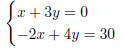
(4,−1)
(−9, 3)
(−8, 5)
(2, 2)
No solution
{(x, y) | x + 3y = 0}
2.
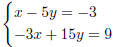
(4,−1)
(−9, 3)
(−8, 5)
(2, 2)
No Solution
{(x, y) | x − 5y = −3}
3.
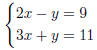
(4,−1)
(−9, 3)
(−8, 5)
(2, 2)
No solution
{(x, y) | 2x − y = 9}
4.
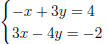
(4,−1)
(−9, 3)
(−8, 5)
(2, 2)
No solution
{(x, y) | −x + 3y = 4}
5.
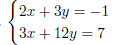
(4,−1)
(−9, 3)
(−8, 5)
(2, 2)
No solution
{(x, y) | 2x+3y = −1}
How did you do?
Solutions to Examples
Example 2.1(a): We substitute the point (−5, 3) into the equation to get
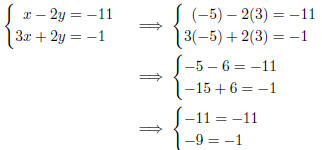
You can see that the first equation is satisfied , but the second equation is
not.
Conclusion: The point (−5, 3) does not satisfy the system.
Example 2.1(b): We substitute the point (−3, 4) into the equation to get
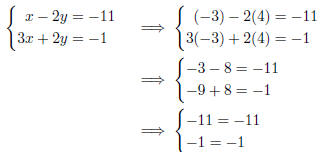
You can see that the both equations are satisfied .
Conclusion: The point (−3, 4) does satisfy the system.
Example 4.1(a): We solve for y in the first equation of
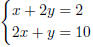to get
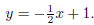We now substitute into the second equation:
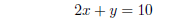second equation
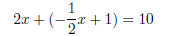substitution
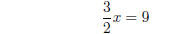combine
and solve
Now substituting x = 6 into the
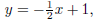we get y = −2.
Solution: These are consistent equations with a unique solution of
(6,−2) , or
the solution set is { (6,−2) } .
Example 4.1(b): We solve for y in the first equation of
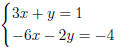to
get y = 1− 3x, and substitute into the second equation:
−6x − 2y = −4
second equation
−6x − 2(1 − 3x) = −4 substitution
−6x − 2 + 6x = −5 combine
−2 = −5 simplify (2)
We see that in equation (2) we get a “false” equation. This means that there is
no solution to the system.
Solution: This is an inconsistent system of equations, there is no solution to
this
system. The solution set is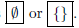 
.
Example 4.1(c): We solve for x in the first equation in
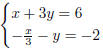to get
x = 6− 3y. Substitute into the second equation:
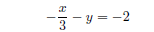second equation
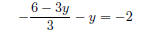substitution
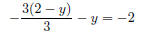factor out 3
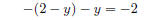combine
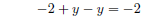deal with the minus sign , correctly
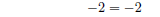simplify again 
(3)
Equation (3) is typical of a dependent system of equations . The equation is
always
true regardless of the value of x . Dependent systems means essentially that
there
are two equations , but each equation is describing the same line.
Solution: This is an consistent system of dependent equations. Any point that
satisfies one of the equations automatically satisfies the the other equation.
Therefore,
the solution set is the set of all points on the satisfy either of the two
equations .
We can write { (x, y) | x + 3y = 6}
Example 4.4(a): To solve
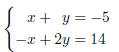
we simply add the two equations together to get 3y = 9, hence, y = 3. From the
first equation, we see that x = −5 − x = −5 −3 = −8.
Conclusion: This is a consistent system of equations with a unique solution of
(−8, 3) .
Example 4.4(b): As discussed earlier, we multiply the first equation by −3:
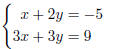given
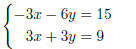multiply by −3
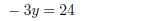add the two equations together
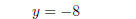solve for y
From the first equation x = −5 − 2y = −5 − 2(−8) = −5 + 16 = 11
Conclusions: This is a consistent system of equations with a unique solution of
(11,−8) .
