INSTRUCTOR:
I. INTRODUCTION
Finite Mathematics is a three semester hour course which covers such topics
as systems of linear equations, linear programming, set theory, counting
techniques, probability, and statistics.
II. OVERALL OR GENERAL OBJECTIVES OF THE COURSE
Upon successful completion of this course, Finite Mathematics, the student
will be able to:
A. Graph quadratic functions and solve business applications of the quadratic
function. (F2, F9)
B. Graph polynomial and rational functions . (F2, F9)
C. Graph exponential functions and solve applications relating to the
exponential function. (F2, F12)
D. Graph logarithmic functions , use the properties of logarithms, and solve
applications of the logarithmic function. (F2, F12)
E. Identify types of sequences and series. (F1, F8)
F. Use sequences and series to solve problems. (F3, F4, F9)
G. Solve finance problems involving simple and compound interest, annuities, and
amortization. (F2, F3, F9)
H. Perform basic matrix algebraic operations . (F3)
I. Solve a system of linear equations by the Gauss-Jordan elimination method and
solve applications relating to systems of linear equations by the Gauss-Jordan
elimination method. (F3, F9)
J. Solve a system of linear equations by using the inverse of the coefficient
matrix. (F2, F3, F9)
K. Solve linear programming problems by the graphical method. (F2, F3, F9)
L. Solve linear programming problems by the simplex method. (F2, F3, F9)
M. Compute the probability of a simple event. (F2, F9, F12)
N. Compute probabilities of compound events using unions and intersections of
events. (F2, F9)
O. Compute conditional probabilities. (F2, F9, F12)
P. Perform basic counting techniques involving permutations and combinations.
(F2, F3, F9, F12)
MATH-1324
Q. Calculate the probability of an event using permutations and combinations.
(F2, F3, F9, F12)
III. INSTRUCTIONAL MATERIALS
The Instructional materials identified for this course are viewable through
IV. COURSE REQUIREMENTS
A. Assignments will be made daily. All assignments are to be completed by
the following class meeting. Assignments may be collected and examined at any
time.
B. Students are expected to attend every class and to arrive at each class on
time and to remain in class for the entire class period. Students who are absent
from class 12.5% of the number of class meetings for any reason will be dropped
from the class with a grade of "F". Instructors may choose to lower a student's
grade because of tardiness.
C. The instructor will post office hours after the semester commences. Consult
the instructor during office hours. If your visit may tend to be lengthy, make
an appointment with the instructor so that he may set aside some time for you.
V. EXAMINATIONS
A. Examinations will be given at the end of each unit. If a unit is short
and simple, it might be included with another short, simple unit for one exam. A
final exam will be given and students must take the final exam in order to pass
the course. The final exam date is announced about two weeks prior to the
examination week.
B. Students who miss an exam should discuss with the instructor the
circumstances surrounding the absence. The instructor will determine whether a
make-up exam is to be given. Make-up examinations are given by appointment only.
VI. SEMESTER GRADE COMPUTATIONS
A. Your point total is determined by adding the points earned on each unit
examination. Your letter grade for the course is then determined by the
following formula:
Your Point Total
Total Points Possible X 100
B. If the result is between 90 and 100 your grade is a(n)
A
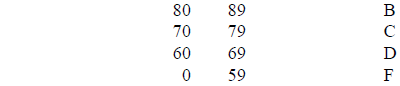
** NOTE: Grade Computation is determined by instructor. Please see your
instructor for how your grade will be determined. This is just an example.
VIII. COURSE OUTLINE
A. Unit One: Functions and Graphs (Chapter 2)
1. Unit Objectives: Upon successful completion of this unit, the student will be
able to:
a. Find the x-intercepts of a quadratic function by using the quadratic formula .
(F2, F9)
b. Graph a quadratic function and locate the maximum or minimum point along with
the zeros of the function . (F2, F9)
c. Use quadratic supply and demand functions to find market equilibrium. (F2,
F9, F12)
d. Solve break-even points by using quadratic cost and revenue functions. (F2,
F9, F12)
e. Maximize quadratic revenue and profit functions. (F2, F9, F12)
f. Graph and apply basic functions, including polynomial and rational functions.
(F2, F9)
g. Graph exponential functions. (F2, F9, F12)
h. Model exponential functions. (F2, F9, F12)
i. Convert equations from logarithmic to exponential form, and vice versa. (F9,
F12)
j. Solve logarithmic equations. (F2, F9)
k. Evaluate some special logarithms. (F2, F3, F9)
l. Graph logarithmic functions. (F2, F9, F12)
m. Simplify expressions involving logarithms by using the properties of logs.
(F2, F9, F12)
n. Compute logarithms using the change of base formula. (F2, F3, F9)
o. Solve exponential growth or decay equations. (F9, F12)
p. Solve exponential equations representing demand, supply, total revenue, or
cost. (F2, F3, F9, F12)
2. Learning Activities:
a. Classroom lecture/discussion
b. Reading assignment
c. Student homework - Study Chapter 2
3. Unit Outline:
a. Section 2.3 (Quadratic Functions)
b. Section 2.4 (Exponential Functions)
c. Section 2.5 (Logarithmic Functions)
B. Unit Two: Mathematics of Finance . (Chapter 3)
1. Unit Objectives: Upon successful completion of this unit, the student will be
able to:
a. Write a specified number of terms of a sequence . (F3, F9)
b. Find a specified terms and sums of specified numbers of terms or arithmetic
sequences. (F3, F9)
c. Find specified terms and sums of geometric sequences. (F3, F9)
d. Find the future value and amount of interest for simple interest loans and
investments. (F3, F9, F12)
e. Find the simple interest rate earned on an investment. (F3, F9, F12)
f. Find the time required for a simple interest investment to reach a goal. (F3,
F9, F12)
g. Find the future value of a compound interest investment and the amount of
interest earned. (F3, F9, F12)
h. Find the annual percentage yield or the effective annual interest rate. (F3,
F9, F12)
i. Find the time it takes for an investment to reach a specified amount. (F3,
F9)
j. Compute the future value ordinary annuities and annuities due. (F9, F12)
k. Compute the payment required of an ordinary annuity and annuity due to have a
specified future value. (F3, F9, F12)
l. Compute the present value of ordinary annuities, annuities due, and deferred
annuities.
m. Compute the payments for a specified present value for a specified present
value for an annuity. (F3, F9, F12)
n. Find the regular payments required to amortize a debt. (F3, F9, F12)
o. Find the amount that can be borrowed for a specified payment. (F3, F9, F12)
p. Develop an amortization schedule. (F3, F9, F12)
2. Learning Activities:
a. Classroom lecture/discussion
b. Reading assignment
c. Student homework-Study Chapter 3
3. Unit Outline:
a. Section 8.1 (Sequences and Summation Notation)
b. Section 8.2 (Arithmetic Sequences)
c. Section 8.3 (Geometric Sequences and Series)
d. Section 3.1 (Simple Interest)
e. Section 3.2 (Compound and Continuous Compound Interest)
f. Section 3.3 (Future Value of an Annuity; Sinking Funds)
g. Section 3.4 (Present Value of an Annuity; Amortization)
C. Unit Three: Systems of Linear Equations; Matrices (Chapter 4)
1. Unit Objectives: Upon successful completion of this unit, the student will be
able to:
a. Add and subtract matrices. (F3)
b. Determine the transpose of a matrix. (F3)
c. Multiply a matrix by a scalar. (F2, F3)
d. Multiply two matrices . (F2, F3)
e. Solve systems of equations by Gauss-Jordan elimination. (F2, F3, F9)
f. Find the inverse of a square matrix . (F2, F3, F9)
g. Use inverse matrices to solve systems of linear equations. (F2, F3, F9)
2. Learning Activities:
a. Classroom lecture/discussion
b. Reading assignment
c. Student homework - Study Chapter 4
3. Unit Outline:
a. Section 4.2 (Systems of Linear Equations and Augmented Matrices)
b. Section 4.3 (Gauss-Jordan Elimination)
c. Section 4.4 (Matrices: Basic Operations)
d. Section 4.5 (Inverse of a Square Matrix)
e. Section 4.6 (Matrix Equations and Systems of Linear Equations)
D. Unit Four: Linear Inequalities and Linear Programming (Chapter 5)
1. Unit Objectives: Upon successful completion of this unit, the student will be
able to:
a. Graph linear inequalities in two variables . (F2, F9, F12)
b. Solve systems of linear inequalities in two variables. (F3, F9, F12)
c. Find the optimum value of a linear function using the geometric approach.
(F3, F9, F12)
2. Learning Activities:
a. Classroom lecture/discussion
b. Reading assignment
c. Student homework - Study Chapter 5
3. Unit Outline:
a. Section 5.1 (Inequalities in Two Variables)
b. Section 5.2 (Systems of Linear Inequalities in Two Variables)
c. Section 5.3 (Linear Programming in Two Dimensions: Geometric Approach)
E. Unit Five: Linear Programming: The Simplex Method (Chapter 6)
1. Unit Objectives: Upon successful completion of this unit, the student will be
able to:
a. Maximize functions subject to constraints using the simplex method. (F9, F12)
b. Determine the dual for minimization problems. (F9, F12)
c. Solve minimization problems using the simplex method on the dual. (F9, F12)
2. Learning Activities:
a. Classroom lecture/discussion
b. Reading assignment
c. Student homework - Study Chapter 6
3. Unit Outline:
a. Section 6.1 (A Geometric Introduction to the Simplex Method)
b. Section 6.2 (The Simplex Method: Maximization with Problem
Constraints of the Form ≤ )
c. Section 6.3 (The Dual Problem: Minimization with Problem
Constraints of the Form ≥ )
F. Unit Six: Introduction to Probability (Chapters 7 & 8)
1. Unit Objectives: Upon successful completion of this unit, the student will:
a. Solve counting problems using the addition principle, multiplication
principle, permutations, and combinations. (F3, F9, F12)
b. Construct a sample space for an experiment. (F3, F9)
c. Compute the probability of a simple event. (F3, F9, F12)
d. Compute the probability of the intersection, union, or complement of events.
(F3, F9, F12)
e. Compute the odds of an event. (F3, F9, F12)
f. Compute the empirical probability that an event will occur. (F3, F9, F12)
g. Solve probability problems involving conditional probability, independent, or
dependent events. (F3, F9, F12)
h. Solve probability problems using counting techniques. (F3, F9, F12)
2. Learning Activities:
a. Classroom lecture/ discussion
b. Reading assignment
c. Student homework – Study Chapters 7 & 8
3. Unit Outline:
a. Section 7.3 (Basic Counting Principles)
b. Section 7.4 (Permutations and Combinations)
c. Section 8.1 (Sample Spaces, Events, and Probability)
d. Section 8.2 (Union, Intersection, and Complement of Events;
Odds)
e. Section 8.3 (Conditional Probability, Intersection, and
Independence)



