Main concepts:
Partial fractions: - Remember that: A prime (i.e. indecomposable)
polynomial (with real coefficients) can only
be either a degree one polynomial or a quadratic that has no real zeros (i.e.
the discriminant b2-4ac < 0). Any
polynomial of degree 3 or higher can still be factored.
- The simple case: all factors in the denominator are linear , and no factors are
repeated. The good thing about
this case is that you can evaluate the constants quite easily by evaluating the
rational function at certain values
of x.
- Second case: Factors in the denominator are all linear but some are repeated.
The decomposition scheme into
simpler fractions is slightly changed. Evaluation of the constants involve
substituting certain (special) values of
x and then trying to get as many equations as the unknowns.
- Third case: Factors in the denominator are linear or prime quadratic. Some
factors are repeated. Very similar
to the second case. Just be careful that when you break it down into simpler
fractions, the numerator part
corresponding to a prime quadratic has to be on the form Ax+B.
Essential skills - Factoring polynomials completely into prime factors.
- Long division of polynomials can be indispensable for some problems.
- Solving linear equations in several unknowns by eliminating the unknowns one
at a time.
- Being able to integrate the the simpler fractions, specially factors with a
prime quadratic in the denominator.
Recall that you may have to complete the square in order to be able to do that.
Sequences: - One very important thing here is to be able to distinguish
between a sequence and a series. A
sequence is a function in n, while a series is an infinite sum of the terms of a
certain sequence.
- Limit problems for sequences do not involve anything new, they are very
similar to limit problems from
Math121.
- Sometimes you have to prove the existence of the limit of a sequence before
trying to evaluate it, say, by using
a recurrence formula. To prove the exitence of the limit, you may use the
theorem we covered in class saying
that a monotone and bounded sequence has to have a limit.
Essential skills - All the skills and tricks you learned in evaluating
limits in Math121 are relevant. Namely,
algebra of limits, L’Hopital’ s rule , the logarithmic trick, dividing both
numerator and denominator by the highest
power of n ...etc.
- Being able to show that a given sequence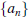 
is (increasing) non-decreasing or (decreasing) non-increasing
by comparing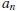 
to
.
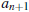Infinite series: - Again, an infinite series,
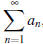, is an infinite sum of terms of a certain
sequence. Convergence
of a series is defined in terms of the convergence of the sequence of partial
sums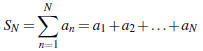 
- Two important examples of series that we know their behavior very well are the
geometric series and telescoping
series. They are among some of the few series that we know their sum in case
they are convergent.
- The nth-term divergence test applies to any series, and can only be
used to prove that a series diverges. You
can NOT use it to prove convergence.
- The absolute convergence test, which states that a
series that is absolutely convergent is also convergent,
can be applied to any series. But you can only use it to prove convergence. You
can NOT use it to prove
divergence. There are countless examples of series that are convergent but not
absolutely convergent. In these
cases, the convergence is due to the fact that the negative terms cancel out
with the positive terms barely evading
divergence.
- Series with positive terms: Infinite series with positive terms are
quite special since their sequence of partial
sums is always increasing (as you keep adding positive terms). By the theorem on
monotone sequences, to prove
that a series with positive tems is convergent, it’s enough to show that its
sequence of partial sums is bounded
from above.
Because of this property , there are several tools (tests) we can use to study
their convergence or divergence.
Namely, the integral test, pth-power test, the direct and limit
comparison tests, and the ratio test.
Intuitively, the convergence of a series with positive terms is just a matter of
how fast the nth-term of the series
approches zero as n → ∞.
- Alternating series: - The alternating series test can be used to prove
convergence of such series. It can never
be used to prove divergence.
- Power series: - Power series is a series that depends on a parameter
(or a variable), say x, and it is on the
form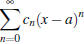 
. Each time you substitute a real number
for x , you get a numeric infinite series. The most
important question is to find all the values of x that yield a convergent
series. The main theorem on power series
paints a very specific picture of what goes on (check your class notes). We can
then use the ratio test to test for
absolute convergence and determine the radius and the interval of convergence.
- Using the formula for the sum of a geometric series, and with some clever
algebraic manipulation, we can
express some functions as the sum of a power series about a given center. This
is a good thing to have, and we
will explore this further later in chapter 8.
- Error estimates: These are essential for numerous real life
applications of infinite series. So far we had two
estimates, the integral test estimate, and the alternating series estimate,
check your notes.
Essential skills - What to do to investigate the convergence or divergence
of a, numeric, series?
In a nut shell: Apply the nth-term divergence test. If it fails,
apply the absolute convergence test, and then
you could use all the tests for series with positive terms. If the absolute
convergence test fails, try to see if the
series is alternating and if the alternating series test applies proving
convergence. For the problems you’ll see
this semester, the above plan should always work. If it doesn’t, then it simply
means that you made a mistake
somewhere, retrace your steps and correct it.
- You have to know how to apply ALL the tests we covered so far. You have to
have a good sense of approximating
the nth term of a series with positive terms in order to gauge how
fast it goes to zero. Then use any of
the comparison tests to prove it.
- When applying the alternating series test, you may have to use some Math121
skills to show that the positive
part of the nth term is decreasing, e.g. as in
.
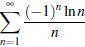Problems: The most important problems to review are, in this specific
order, your homework problems, examples
done in class, and problems on the quizzes. The following set of problems is a
just collection of particularly
tough questions to serve the purpose of reviewing as many concepts as possible.
They do not necessarily represent
the questions you will see on the exam. The problems on the exam will be much
closer to the ones from
your homework, or the ones we did in class than the ones found here.
Good luck, see you on Monday if you have any questions.
(1) Evaluate the following limits.
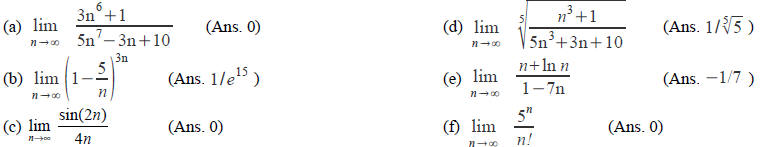
(2) Which of the following series converge and which
diverge? Justify your answer by naming the tests you are using.
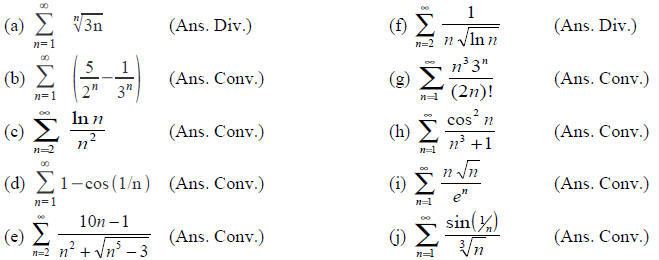
(3) Find the interval and radius of convergence for each
of the following power series. Justify your answer
(4) Find the value a for which the following series
converges to 2/3 .
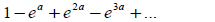(Ans. -ln2)
(Food for thought: Could we ask the same question and have
the sum be equal to 
instead of
?)
(5) Is it possible to write the function
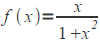as the sum of a power series about x=0 ?
Explain your answer,
and find the values of x that make this possible?
(6) Expand each of the following quotients by partial fractions
 |
 |
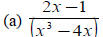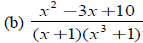(Answer:  ) |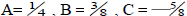
(Answer: A=3 , B =14, C =-3 , D =-7 ) |
