We’re going to arrange the positive rational numbers in a
list that begins like this :
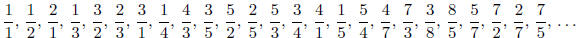
Some of the interesting features of this list are
1. The denominator of each fraction is the numerator of the next one. That means
that the
nth rational number in the list looks like f(n)/f(n+1) (n = 0, 1, 2, . . .),
where f is a certain
function of the nonnegative integers whose values are
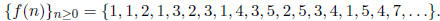
2. The function values f(n) actually count something nice.
In fact, f(n) is the number of
ways of writing the integer n as a sum of powers of 2, each power being used at
most twice
(i.e., once more than the legal limit for binary expansions). For instance, we
can write
5 = 4 + 1 = 2 + 2 + 1, so there are two such ways to write 5, and therefore f(5)
= 2. Let’s
say that f(n) is the number of hyperbinary representations of the integer n.
3. Consecutive values of this function f are always relatively prime, so that
each rational occurs
in reduced form when it occurs.
4. Every positive rational occurs once and only once in this list.
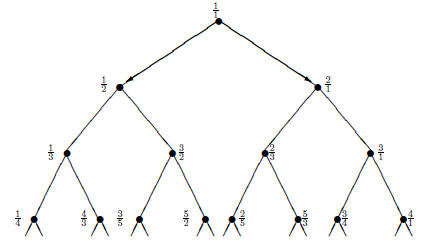
Figure 1: The tree of fractions
1 The tree of fractions
For the moment, let’s forget about enumeration, and just imagine that fractions
grow on the tree
that is completely described, inductively, by the following two rules:
• 
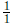( the root ) is at the top of the tree, and
• Each vertex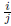 
has two children: its left
child is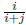 
and its right child is
.
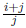We show the following properties of this tree .
1. The numerator and denominator at each vertex are relatively prime. This is
certainly true at
the top vertex. Otherwise, suppose r/s be a vertex on the highest possible level
of the tree
for which this is false. If r/s is a left child, then its parent is r/(s − r),
which would clearly
also not be a reduced fraction, and would be on a higher level, a contradiction.
If r/s is a
right child, then its parent is (r − s)/s, which leads to the same
contradiction.
2. Every reduced positive rational number occurs at some vertex. The rational
number 1 certainly
occurs. Otherwise, let r/s be, among all fractions that do not occur, one of
smallest
denominator, and among those the one of smallest numerator. If r > s then
(r−s)/s doesn’t
occur either, else one of its children would be r/s, and its numerator is
smaller, the denominator
being the same, a contradiction. If r < s, then r/(s − r) doesn’t occur either,
else one
of its children would be r/s, and it has a smaller denominator, a contradiction.
3. No reduced positive rational number occurs at more than one vertex. First,
the rational
number 1 occurs only at the top vertex of the tree, for if not, it would be a
child of some
vertex r/s. But the children of r/s are r/(r + s) and (r + s)/s, neither of
which can be 1.
Otherwise, among all reduced rationals that occur more than once, let r/s have
the smallest
denominator, and among these, the smallest numerator. If r < s then r/s is a
left child of
two distinct vertices, at both of which r/(s − r) lives, contradicting the
minimality of the
denominator. Similarly if r > s.
It follows that a list of all positive rational numbers, each appearing once and
only once, can be
made by writing down 1/1, then the fractions on the level just below the top of
the tree, reading
from left to right, then the fractions on the next level down, reading from left
to right, etc.
We claim that if that be done, then the denominator of each fraction is the
numerator of its
successor. This is clear if the fraction is a left child and its successor is
the right child, of the same
parent. If the fraction is a right child then its denominator is the same as the
denominator of its
parent and the numerator of its successor is the same as the numerator of the
parent of its successor,
hence the result follows by downward induction on the levels of the tree.
Finally, the rightmost
vertex of each row has denominator 1, as does the leftmost vertex of the next
row, proving the
claim.
Thus, after we make a single sequence of the rationals by reading the successive
rows of the tree
as described above, the list will be in the form
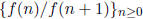, for some f.
Now, as the fractions sit in the tree, the two children of f(n)/f(n+1) are
f(2n+1)/f(2n+2)
and f(2n + 2)/f(2n + 3). Hence from the rule of construction of the children of
a parent, it must
be that
f(2n + 1) = f(n) and f(2n + 2) = f(n) + f(n + 1) (n = 0, 1, 2, . . .).
These recurrences evidently determine our function f on all nonnegative
integers.
We claim that f(n) = b(n), the number of hyperbinary representations of n, for
all n ≥ 0.
This is true for n = 0, and suppose true for all integers ≤ 2n. Now
b(2n+1) = b(n), because if
we are given a hyperbinary expansion of 2n+1, the “1” must appear, hence by
subtracting 1 from
both sides and dividing by 2, we’ll get a hyperbinary representation of n.
Conversely, if we have
such an expansion of n, then double each part and add a 1, to obtain a
representation of 2n + 1.
Furthermore, b(2n + 2) = b(n) + b(n + 1), for a hyperbinary expansion of 2n + 2
might have
either two 1’s or no 1’s in it. If it has two 1’s, then by deleting them and
dividing by 2 we’ll get an
expansion of n. If it has no 1’s, then we just divide by 2 to get an expansion
of n+1. These maps
are reversible, proving the claim.
It follows that b(n) and f(n) satisfy the same recurrence formulas and take the
same initial
values, hence they agree for all nonnegative integers. We state the final result
as follows.
Theorem 1 The nth rational number, in reduced form,
can be taken to be b(n)/b(n + 1), where
b(n) is the number of hyperbinary representations of the integer n, for n = 0,
1, 2, . . .. That is, b(n)
and b(n + 1) are relatively prime, and each positive reduced rational number
occurs once and only
once in the list b(0)/b(1), b(1)/b(2), . . ..
2 Remarks
There is a large literature on the closely related subject of Stern-Brocot trees
[Ste, Bro]. In particular,
an excellent introduction is in [GKP], and the relationship between these trees
and hyperbinary
partitions is explored in [Rez]. In Stern’s original paper [Ste] of 1858 there
is a structure that is essentially
our tree of fractions, though in a different garb , and he proved that every
rational number
occurs once and only once, in reduced form. However Stern did not deal with the
partition function
b(n). Reznick [Rez] studied restricted binary partition functions and observed
their relationship to
Stern’s sequence. Nonetheless it seemed to us worthwhile to draw these two
aspects together and
explicitly note that the ratios of successive values of the partition function
b(n) run through all of
the rationals.
