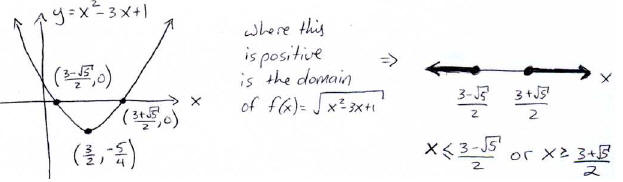Memorize: The two solutions to the
equation ax2 + bx + c = 0 are given by the quadratic formula: |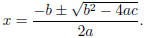
Example 9.2.25 Solve
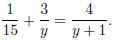
(multiply by the LCD
which is 15y(y + 1))
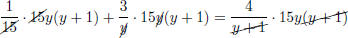( simplify )
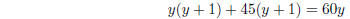
(use quadratic formula –I always write it
out)
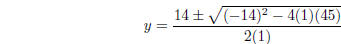
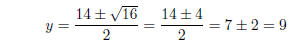or y = 5
Since neither y = 9 nor y = 5 makes the LCD zero , these
are both solutions.
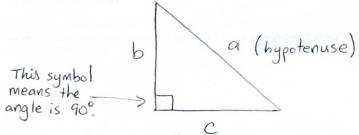
Pythagorean Theorem
• The hypotenuse in a right triangle is the side opposite the 90 degree angle in
the triangle.
• Pythagorean theorem: a2 = b2 + c2, where a is
the length of the hypotenuse in a right triangle and b and c are the
lengths of the other two sides .
Sketching Quadratics
• For a quadratic y = f(x) = ax2 + bx + c, we have
• x-intercepts: determine these by using the quadratic formula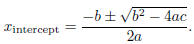
NOTE: If b2 − 4ac < 0 then there are no x-intercepts (they are not
real numbers).
• Vertex: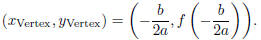 
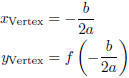
How to remember this: The x- coordinate of the vertex will
be right in the middle of the two x-intercepts, even if
the x- intercepts are not real numbers !
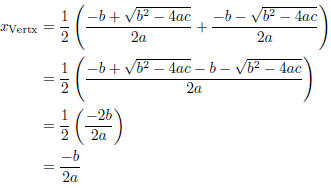
• y-intercept: evaluate at x = 0, so figure out what f(0)
is.
• The function opens up if a > 0, and opens down if a < 0.
Example Sketch the parabola y = 5x2 + 4x − 12. Label the
vertex, y-intercept, and any x-intercepts on your sketch.
To get the sketch of a quadratic, we should do four things:
• Determine if it opens up or down,
• Determine the vertex,
• Determine any x-intercepts (if they exist),
• Determine the y-intercept.
A quadratic opens up if a > 0, and opens down if a < 0. Since a = 5 in this
case, this quadratic opens up.
To get the vertex, identity a = 5, b = 4, and c = −12. Then the vertex is
located at:
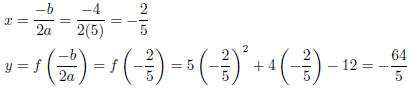
The vertex is at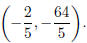 
To get the x-intercepts, use the quadratic formula:
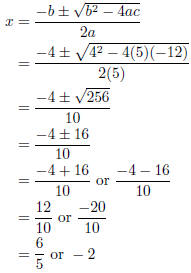
To get the y-intercept, evaluate f(0):
y = f(0) = 5(0)2 + 4(0) − 12 = −12
You can now put this all together to get the sketch:
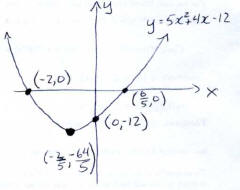
Solving power equations
1. Algebraically isolate the power portion on one side of equal sign .
2. Use an appropriate radical on each side of the equation to remove the power.
Include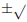 
in square roots .
3. Solve the equation.
4. Check all solutions, and exclude any that do not satisfy the original
equation. These excluded solutions are called
extraneous solutions.
An alternate (and sometimes much easier) technique is to expand the power terms ,
and then collect like terms and try
to factor the new expression to find the solutions . If the powers are squares,
you can always do this with the aid of the
quadratic formula.
Solving Absolute Value Equalities and Inequalities: Three Cases
Case1 For equalities of the form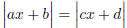 
,
the solution is
ax + b = cx + d or ax + b =- (cx + d).
The solution will be two distinct numbers.
Case2 For inequalities of the form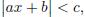 
where c > 0 the solution is
−c < ax + b < c.
NOTE: it is important that the −c is on the left and the c is on the right. If
this isn’t the case, you will get the wrong
solution.
The solution will be a set of points between two numbers.
Case3 For inequalities of the form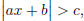 
where c > 0 the solution is
ax + b < −c or ax + b > c.
The solution will be a set of numbers less than one number or greater than
another number.
Example Solve the inequality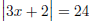 
and
sketch the solution on a number line.
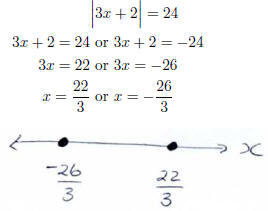
Example Solve the inequality
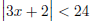and sketch the solution on a number line.
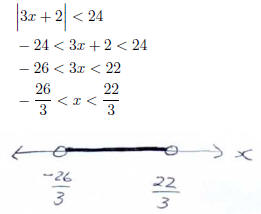
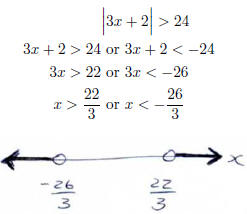
Example Solve the inequality
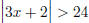and sketch the solution on a number line.
Example What is the domain of the function
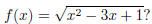Sketch your answer on a number line.
Domain: what real numbers can I put into this expression and get a real number
out?
x2 − 3x + 1 ≥0
We only know how to algebraically solve linear inequalities , but we can sketch y
= x2 − 3x + 1 and get the answer from
our sketch by figuring out where x2 − 3x + 1 is positive.
Since a = 1 > 0, this quadratic opens up.
To get the vertex, identity a = 1, b = −3, and c = 1. Then the vertex is located
at:
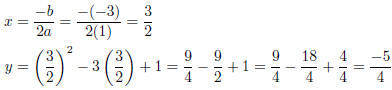
The vertex is at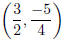
.
To get the x-intercepts, use the quadratic formula:
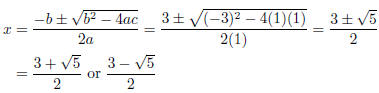
We don’t need the y-intercept to answer the question. You
can now put this all together to get the sketch:
