Practice Test Explanations: Mathematics
1.Correct Response: D. To solve this problem, you must multiply the
number of bottles
capped per second times the total number of seconds in I 5 hours:
(3 bottles/sec) (60 sec/min) (60 min/hr) (15 hr)
l .6 x l05 bottles
Notice that all the units cancel except the number of bottles. Choice A results
from
omitting one of the factors of 60. Choice B results from miscounting the number
of
decimal places in the answer. Choice C results from interpreting the problem as
saying
"3 seconds per bottle" instead of "3 bottles per second."
2.Correct Response A. To solve this problem, first add the total number
of gallons of
gas used, then subtract that number from the initial number of gallons:
Choice B results from adding incorrectly. Choice C results
from adding only the integer
parts of each number. Choice D is the total number of gallons of gas used.
3. Correct Response: C. This is a multistep problem
involving subtraction, percents, and
addition. First find how much fencing is left after the morning, then find 40%
of this
remaining fencing, then add those two numbers:
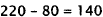 |
Subtract. |
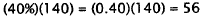 |
Multiply. |
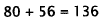 |
Add. |
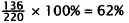 |
Find percentage, |
Choice A is the percent of fencing that was put up in the
morning. Choice B is the-result
of adding the amount of fencing put up in the morning plus 4O% of the amount of
fencing put up in the morning. Choice D is the result of adding the amount of
fencing
put up in the morning plus 40% of the original amount of fencing to be put up.
4. Correct Response: B. This problem is solved by
using proportions.
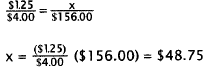
Choice A results from subtracting $I.25 from $4.00. Choice
C results from multiplying
$1.25 times $156.00. choice D results from setting up the proportion
incorrectly.
5. Correct Response: A. This problem involves
taking a percentage of a percent. Eighteen
percent of the advertising expenditures (which is 35% of the total budget) is
spent on
radio advertising.
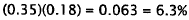
Choice B results from calculating I 8% of the
non-advertising expenditures. Choice C
is the percentage of advertising expenditures spent on radio advertising. Choice
D
is the percentage of total expenditures spent on advertising.
6. Correct Response: A. Solving this problem involves correctly interpreting
the
information on the graph. At time t = 0, the pond is stocked with a certain
number of
fish. This eliminates choice D, since on that graph there are no fish in th6
pond initially.
The number of fish steadily decreases. This eliminates choice C, since that
graph shows
the number of fish remaining constant through time. (this also eliminates choice
D,
since that graph shows the number of fish as increasing through time.)
Eventually, there
are approximately half the number of fish originally stocked. This eliminates
choice B,
since on that graph, the number of fish is never half the number of fish
initially
stocked.
7 . Correct Response: B. To solve this problem, let
x equal the test score needed. Then,
since the test counts twice as much as the quizzes, x must appear twice in the
expression for the average:
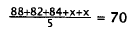 |
|
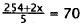 |
Simplify |
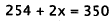 |
Multiply by 5. |
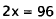 |
Subtract 254. |
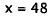 |
Divide by 2. |
Choice A results from including x twice, but dividing by 4
instead of 5. (There are 5
grades to be counted: 3 quizzes, and the test grade, twice.) Choice C is the
average
the student needs, not the test score. Choice D results from only counting x
once, but
dividing by 5.
8.Correct Response: C. Solving this problem involves correctly interpreting
a distribution
graph. The mean of a (symmetric) distribution curve is where it attains its
maximum
value. Both curves in the graph have approximately the same mean, which
eliminates
choices A and D. The distribution curves give the percentage of cars that have a
given
gas mileage, which eliminates choice B. The variability of the data is reflected
in the
width of the distribution curve. Since curve A is narrower than curve B, brand A
cars
have smaller variability in gas mileage than brand B cars.
9.Correct Response: A. Solving this problem involves correctly
interpreting information
from the graph of a line. The slope- intercept form of a line is y = mx + b,
where m is
the slope of the line and b is the y-intercept. The y-intercept of the given
line is 2, which
eliminates choices B and C. The slope of the line is:
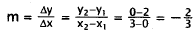
Choice D has slope m = 3. Only choice A fits both
criteria.
10. Correct Response: B. The slope of the line
through two points is:
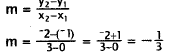
Choice A results from calculating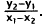
Choice A results from calculating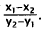
Choice A results from calculating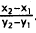
I I . Correct Response: B. This problem involves
finding the slope of the line, and then
substituting the coordinates of a point on the line to eliminate the incorrect
answers.
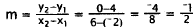
This eliminates choice A, which has m = 1/2 , and choice
C, which has m = -2. Of the
remaining two choices, only choice B passes through both given points:
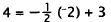 |
Substitute -2 for x and 4 for Y. |
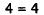 |
|
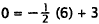 |
Substitute 6 for x and 0 for Y. |
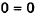 |
|
12.Correct Response: B. To solve this problem, you
must recognize that the graph
represents an inverse variation relation. lf a rectangle has constant area, then
length x width = constant, or 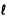 w = constant.
The graph passes through the point (3,4)
w = constant.
The graph passes through the point (3,4)
so that, at that point, 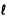 = 3 and w = 4.
Therefore, the constant for this rectangle is
= 3 and w = 4.
Therefore, the constant for this rectangle is
3 ·4= 12. Now, if 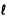 =8,then 8w =12 or
=8,then 8w =12 or
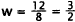 .Choice A results from incorrectly
.Choice A results from incorrectly
estimating the w-value of the graph at  = 8.
Choice C results from subtracting 12 - 8
= 8.
Choice C results from subtracting 12 - 8
instead of dividing l2/8. Choice D results from multiplying (12)(8) instead of
dividing
12/8.
13.Correct Response: C. This problem requires
determining the value of an unknown in an
equation and using that value to solve a second problem. The first step is to
solve the
first equation for x.
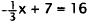 |
|
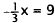 |
Subtract 7 from each side. |
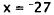 |
Multiply each side by - 3. |
Now, use x = -27 in the second problem.
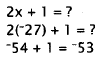
Choice C, -53, is correct. Choice A, -5, results from
multiplying the right side by -1/3
instead of -3. Choice B, -27, results from solving only the first equation.
Choice D, -137,
results from adding rather than subtracting 7 in the first problem-solving step.
14. Correct Response: A. This problem involves
finding the value of an unknown in an
equation and expressing it in terms of another unknown . To find the value of t
in terms
of r, the first step is to isolate t on one side of the equation.
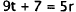 |
|
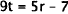 |
Subtract 7 from each side. |
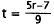 |
Divide each side by 9. |
Choice B results from a sign error when subtracting 7 from
both sides. Choice C results
from dividing only one term, rather than both, by 9. Choice D results from both
of the
above errors.
I 5. Correct Response: B. This problem involves
solving two equations simultaneously,
one of which is quadratic, and the other of which is linear. We may solve this
system
of equations by substitution. Since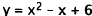 (first
equation), substitute
(first
equation), substitute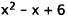
for y in the second equation, and solve that equation for x:
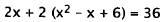 |
Substitute. |
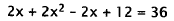 |
Distribute. |
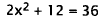 |
Simplify. |
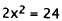 |
Subtract I 2. |
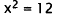 |
Divide by 2. |
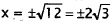 |
Take the square root. |
Now solve for y:
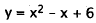 |
|
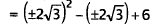 |
Substitute for x. |
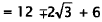 |
Simplify. |
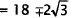 |
Simplify. |
Therefore, 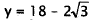 when
when
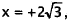 ,and
,and 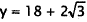 when
when
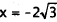 ,The correct
,The correct
answer, then, is 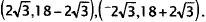 In choice A, (0,6) is a
solution of the
In choice A, (0,6) is a
solution of the
first equation, and (9,9) is a solution of the second equation, but they are not
solutions
of both equations simultaneously.
16. Correct Response: C. This problem involves
solving two simultaneous equations
in two variables by graphing. The first equation is a line with slope m = -2 and
y-intercept b = -2:
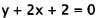 |
|
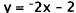 |
Solve for y. |
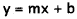 |
Slope-intercept form of a line. |
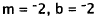 |
By inspection. |
Since the slope is negative , the graph of the line slopes
down and to the right. This
eliminates choices A and B, since both lines have positive slopes. The second
equation
is a parabola that opens up (since y = ax2 + bx + c with a>0 is a
parabola that opens
up). This eliminates choice D. Only choice C fits all of the properties of the
two
equations.
17. Correct Response: B. This problem involves
writing algebraic relationships from verbal
descriptions. The sum of x and y is x + y, and the product of x and y is xy. The
quotient of
these two expressions is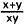 ,and the square of
this quotient ,
,and the square of
this quotient ,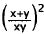 . Ten more
. Ten more
than this expression 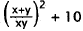 , which is equal to C.
Choice A is the square of I 0
, which is equal to C.
Choice A is the square of I 0
more than the quotient of the sum of x and y and the product of x and y. Choice
C is
I 0 more than the square of the quotient of the product of x and y and the sum
of x and
y. Choice D is l0 more than the quotient of the square of the sum of x and y,
and the
product of x and y.
18. Correct Response: A. The difference of m2 and n is m2
- n, and the square of this
expression is (rn2 - n)2. fifty less than this expression
is (m2 - n)2 - 50, which equals P.
Choice B is 50 less than the difference of m2 and n. Choice C is the
square of 50 less
than the difference of m2 and n. Choice D is the difference of 50 and
the square of the
difference of m2 and n.
19. Correct Response C. This problem involves
writing an algebraic expression for the
relationships between the lengths of the three pieces of the board. Let the
lengths of
the three pieces be a, b, and c. Then, the sum of the lengths of the three
pieces is I 0
feet: a + b + c = 10. But the second piece (b) is not as long as the first (a):
b =a/2 . And,
the third piece (c) is 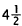 feet longer than the
second (b or a/2 ):
feet longer than the
second (b or a/2 ):
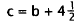 |
|
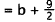 |
Simplify:
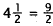 |
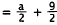 |
Substitute for b. |
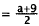 |
Combine fractions. |
Now substitute back into the first equation:
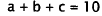 |
|
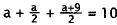 |
Substitute for band c. |
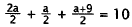 |
Common denominator. |
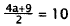 |
Combine fractions. |
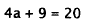 |
Multiply by 2. |
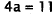 |
Subtract 9. |
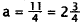 |
Divide by 4. |
Choice A results from using the incorrect relation that
the second piece is twice as long
as the first. Choice B results from using the incorrect relation that the third
piece is 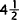
feet longer than the first piece. Choice D results from dividing the l0-foot
board into
three equal pieces.
20. Correct Response A. This problem involves writing relations between
different
quantities as a system of three linear equations in three variables. lf we write
all money
quantities in cents, then Angel has I 80 cents in his pocket. The total number
of cents
in nickels is 5N (5 cents for each nickel, times the number of nickels N), the
total
number of cents in dimes is 10D (10 cents for each dime, times the total
number of
dimes D), and the total number of cents in quarters is 25Q (25 cents for each
quarter
times the number of quarters Q). This gives the first equation: 5N + l0D + 25Q =
I 80.
This excludes choices C and D. Since the coefficients on the left side and the
number
'on the right side are written in different units (cents and dollars). The
second sentence
says that Angel has twice as many quarters as nickels, so that the number of
quarters Q
is two times the number of nickels N. Q = 2N. This excludes choice B, in which
the
relation is reversed. The third sentence says that the number of dimes D equals
the
number of nickels N plus the number of quarters Q plus I : D = N + Q+ l. Only
choice A
has all three of these equations.
Correct Response: B. This problem involves writing an equation from the
given verbal
information, and solving it. lf $175 was collected this week, and this was $35
more
than was collected last week, then $175 - $35 = $140 collected last week. The
total
amount of money collected in the two weeks, then, was $140 + $I75 = $315. Choice
A
assumes that $35 was collected in the first week. Choice C assumes that $35 less
was
collected in the second week than in the first week. Choice D assumes that $70
less was
collected. in the second week than in the first week.
22. Correct Response: C. To solve this problem, you must factor the
quadratic expression.
The factors of 24 are 1 ·24, 2 ·12, 3· 8, and 4 · 6. One of each pair of factors
must be
positive and the other negative, since the constant term is negative (-24):
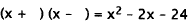
The only pair of factors that sums to -2 (the coefficient
of x) is +4, -6:
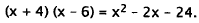
Choice A is the result of factoring incorrectly. Choices B
and D are the results of
choosing the wrong signs to the factors.
23. Correct Response: D. This problem may be solved
by inverting the second rational
expression and factoring, then simplifying and multiplying.
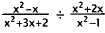 |
|
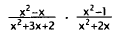 |
lnvert the second expression and change division
to
multiplication. |
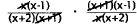 |
Factor and cancel. |
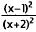 |
Simplify. |
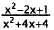 |
Multiply out. |
Choice A results from multiplying the two rational
expressions instead of dividing.
Choice B results from canceling before inverting the second expression, then
inverting
and canceling again. Choice C results from incorrectly canceling and
multiplying.
24. Correct Response: A. This problem involves
simplifying a rational expression.
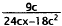 |
|
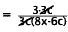 |
Factor 3c out of expressions in numerator and
denominator. |
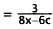 |
Cancel 3c. |
Choice B results from correctly canceling the c but
subtracting coefficients instead
of factoring and canceling. Choice C results from taking the reciprocal of the
correct
answer. Choice D results from correctly canceling the c but incorrectly
canceling the
coefficients.
25. Correct Response: D. This problem involves dividing and simplifying
two rational
expressions, and using the laws of exponents.
Choice A results from multiplying the two expressions
instead of dividing. Choice B
results from correctly inverting the second expression and adding exponents of
common bases in the denominator, but then multiplying exponents instead of
subtracting in the last step. Choice C results from correctly inverting and
adding
exponents of common bases in the denominator, but then dividing exponents
instead of subtracting in the last step.
26. Correct Response: C. This problem involves
evaluating a function for a particular value
of its variable.
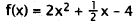 |
|
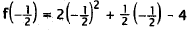 |
Substitute -1/2 for x. |
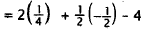 |
square (-1/2). |
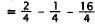 |
Simplify and rewrite last term using common
denominator of 4. |
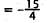 |
Simplify. |
Choice A is f(1/2). Choice B is f(2). Choice D is f(-2).
27.Correct Response: B This problem involves determining the equation of
a function
from its graph. The graph is a parabola that opens up so that it has the form
Y = ax2 + bx + c where a is positive. This eliminates Choices A and
C. The graph
passes through the points (-2,0), (3,0) (the x-intercepts), and (0,-6) (the
y-intercept).
The only choice in which substituting these values for x and y makes the
equation
true is choice B.
28.Correct Response: C. This problem involves identifying an inequality
from its graph.
To solve this problem first identify the equality. The graph is a parabola
opening down,
that passes through the points (0,0), (1,1 ), and (2,0). Only choices B or C,
when written
as equalities, satisfy all three of these points when the coordinates are
substituted into
the equations. To determine which choice is correct, pick a point inside the
shaded
region and substitute the coordinates into the expression, leaving a question
mark for
the inequality sign:
Zero is less than one, so choice C is correct.
29. Correct Response: D. This problem requires
carrying out a step in solving a quadratic
equation by completing the square. To complete the square, make sure the
coefficient
of x2 is l, take half the coefficient of x, square it and place the
result in each set of
parentheses.
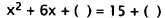 |
|
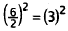 |
Half of coefficient of x is 3. |
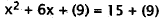 |
Place 9 in each set of parentheses. |
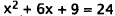 |
First three terms are a perfect square. |
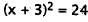 |
|
Choice A results from taking one half of one half the
coefficient of x. Choice B results
from taking half the coefficient of x, but not squaring it. Choice C results
from
incorrectly squaring 3,
30. Correct Response: B. To solve this problem, you
must first put the expression in
standard form and then use the quadratic formula:
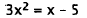 |
|
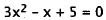 |
Bringx-5toleftside. |
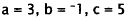 |
Coefficients. |
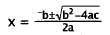 |
Quadratic formula. |
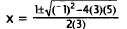 |
Substitute for a, bi and c. |
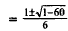 |
|
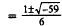 |
|
Choice A results from incorrectly putting the expression
in standard form, and uses
3x2 + x - 5 = 0. Choice C results form an incorrect use of the
quadratic equation
(b2 + 4ac instead of b2 - 4ac). Choice D results from an
incorrect use of the quadratic
equation (4ac - b2 instead of b2 - 4ac).
31. Correct Response: B. This problem involves using the quadratic model
to solve for a
particular value of one of the variables. To solve this problem, substitute
known height
for h and solve for t:
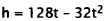 |
|
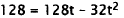 |
Substitute | 28 for h. |
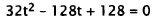 |
Put in standard quadratic form. |
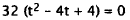 |
Factor out 32. |
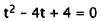 |
Divide by 32. |
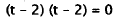 |
Factor. |
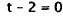 |
Zero factor rule. |
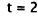 |
Add 2 to both sides. |
Choice A results from an error made inputting the equation
in standard quadratic form.
Choice C results from incorrectly factoring. Choice D results from incorrectly
solving
the quadratic equation.
32. Correct Response: B. To solve this problem, the total area of the
geometric figure must
be calculated. This is best done piece by piece. The area of the lower
rectangular part of
the window is 6 ft. x 4 ft. = 24 square feet. The area of the upper triangular
part of the
window is:
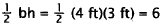 square feet.
square feet.
The total area is the sum of the two sections: 24 square feet + 6 square feet =
3O
square feet.
Choice A is the area of just the rectangular lower section of the window. Choice
C is the
area the window would have if it were a rectangle 4 feet wide and 9 feet high.
Choice D
is twice the area of the rectangular lower section of the window.
33. Correct Response: C. To solve this problem, you
must calculate the perimeter of the
figure, including the two semicircular end caps, and then multiply by 8 for the
8 laps.
There are two straight parts of the track, each 200 m long, for a total of 400
m. Each
end cap is a semicircle, making a full circle of radius 25 m. The circumference
of
the circle is 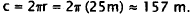 The total perimeter of the
track, then, is
The total perimeter of the
track, then, is
approximately 400 m + 157 m = 557 m. The runner runs 8 times around, for a total
of 8 x 557 m= 4456 m. Choice A is the approximate length of one lap. Choice B is
the length of 8 laps around a rectangular track measuring 200 m x 50 m. Choice D
counts each end cap as a full circle instead of a semicircle.
34. Correct Response: D. This problem involves knowing the formula for the
surface of a
sphere. The surface area of a sphere of radius r is
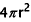 . Therefore, the surface area of
. Therefore, the surface area of
a hemisphere is half that of a sphere: 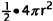 .tfahemisphereisdividedintol2equal
.tfahemisphereisdividedintol2equal
sections, each section has 1/12 of the area of the hemisphere:
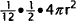 . if the radius
. if the radius
of the hemisphere is l8 m, the formula for one section of the hemisphere is
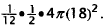 Choice A is the formula for 1/12 the volume
of a hemisphere of radius
Choice A is the formula for 1/12 the volume
of a hemisphere of radius
I 8 m. Choice B is the formula for the entire surface area of a hemisphere of
radius
18 m. Choice C is an incorrect formula, since it uses the square of the diameter
of the
hemisphere instead of the radius
35. Correct Response: C. Solving this problem involves using the Pythagorean
theorem.
The ramp forms the hypotenuse of a right triangle whose base is the ground, and
whose vertical side is the wall of the platform:
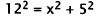 |
Pythagorean Theorem. |
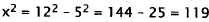 |
Solve for x2. |
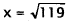 |
Square root. |
Choice A is the difference between the length of the ramp
and the height of the
platform. Choice B is the average of the length of the ramp and the height 9f
the
platform. Choice D is the hypotenuse of a triangle whose sides have lengths 5
and 12.
36. Correct Response: D. To solve this problem, you must use the
properties of similarity
to set up a proportion between two pairs of sides of the two figures.
Corresponding
sides of the two figures are proportional:
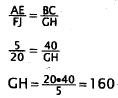
Choice A results from incorrectly setting up the
proportion. Choice B results from
adding the lengths of the two sides of the first figure, and equating that
number
to the sum of the lengths of the two sides of the second figure. This is
incorrect
because in similar geometric figures, the lengths of corresponding sides are
proportional, but the sides do not necessarily add up to the same lengths.
Choice C
is the sum of the lengths of the two given sides of the first figure.
37. Correct Response: C. To solve this problem, you
must use the properties of similarity
to set up a proportion between two pairs of sides of the two figures.
corresponding
sides of the two figures are proportional:
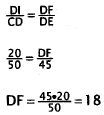
Choice A results from setting up the proportion
incorrectly. Choices B and D result from
assuming that the lengths of the two pairs of sides sum to the same number. In
similar
geometric figures, the ratios of corresponding sides are equal, but the lengths
of the
sides of the two figures do not necessarily sum to the same number.
38. Correct Response: C. To solve this problem, you must use the
properties of parallel
lines. In the figure, angle k and angle w are corresponding angles, so that the
measure
of angle k equals the measure of angle w. Angle w and angle y are supplementary
angles, since they lie on the straight line. Supplementary angles add to 180°.
Therefore,
the measure of angle k plus the measure of angle y is I 80°.
Choice A results from incorrectly using angle w and angle y as complementary
angles.
Choice B results from incorrectly summing supplementary angles to be 100°.
Choice D
results from summing angles k, j, m, and n.
39. Correct Response: C. To solve this problem, you need to use the
properties of triangles
and of parallel lines. The angles of a triangle add up to 180°. An equilateral
triangle has
three equal angles, so that each angle is 60°. Therefore, the measure of angle 3
is 60°.
Since line BC is parallel to line CE, angles 3 and 4 are corresponding angles.
The
measure of angle 4 is 60°, since corresponding angles are congruent. Angles 4
and 5
are supplementary angles, since they lie on a straight line. Supplementary
angles add
up to 180°. Therefore,
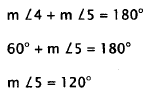
Choice A is the measure of angle 4. Choice B is the
measure of a right angle, and
Choice D is the sum of angle 4 and angle 5.
40. Correct Response: A. This problem involves an
application of inductive reasoning.
Since Carl has brown hair (by statement 5), Carl must like pizza (by statement
3).
Choice B (Carl has red hair) cannot be true since he has brown hair (by
statement 5). We
do not know whether Carl is wearing a hat (choice C). lt is true that Carl has
brown hair
(statement 5), but there is no statement saying that all people who have brown
hair are
wearing hats. Statement I says that all people wearing hats have brown hair. We
do not
know whether Carl likes hamburgers (choice D). There is no statement that says
that
people who have brown hair like hamburgers, though there is one (statement 4)
that
says that people who have red hair like hamburgers.
41 . Correct Response: A. This problem involves an application of
inductive reasoning,
in this case determining the missing design from a pattern sequence. This type
of
problem is solved by using the given information to determine how the pattern
changes, and then predicting what the missing design should be. The pattern is
discerned
by trial and error. ln this case, the pattern is that the external shape becomes
the internal shape of the design to its right (or vice versa). Since the
external shape of
the design to the left of the blank is a diamond, that must be the internal
shape of the
correct response. Since the internal shape of the design to the right of the
blank is a
semicircle, that must be the external shape of the correct response. Adding
together
these two shapes gives choice A. Choices B, C, and D are designs that do not fit
in the
pattern sequence.
42. correct Response B. This question involves the
application of deductive reasoning
to solve a given problem. This problem is best solved by setting up a matrix
using the
persons as one dimension and the jobs as the other.
| |
Writer |
Researcher |
Artist |
Engineer |
| Bess |
|
|
|
|
| Tara |
|
|
|
|
| Gerard |
|
|
|
|
| Clifton |
|
|
|
|
Then, using the given statements, fill in the matrix.
Since the information is in the
form of who is not what (e.9., Bess and Gerard are not the engineer), put an X
in the
appropriate places to rule out the jobs each person cannot hold. For statement
l, Bess
and Gerard cannot be the engineer.
| |
Writer |
Researcher |
Artist |
Engineer |
| Bess |
|
|
|
x |
| Tara |
|
|
|
|
| Gerard |
|
|
|
x |
| Clifton |
|
|
|
|
Add statement ll, which indicates that Clifton and Tara cannot be the
researcher.
| |
Writer |
Researcher |
Artist |
Engineer |
| Bess |
|
|
|
x |
| Tara |
|
x |
|
|
| Gerard |
|
|
|
x |
| Clifton |
|
x |
|
|
Finally, add statement lll, which indicates that Gerard
cannot be the writer or the
researcher.
| |
Writer |
Researcher |
Artist |
Engineer |
| Bess |
|
|
|
x |
| Tara |
|
x |
|
|
| Gerard |
x |
x |
|
x |
| Clifton |
|
x |
|
|
The only empty cell under researcher corresponds with Bess;
therefore, choice B must
be correct.
43. Correct Response: C. This problem involves an
application of inductive reasoning,
in this case determining the missing design from a pattern sequence. This type
of
problem is solved by using the given information to determine how the pattern
changes, and then predicting what the missing pattern should be. In this case,
the
designs are polygons with different numbers of sides, so the first step is to
write
down the number of sides in each polygon:
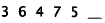
This is two sequences mixed together. Every other term in
the sequence increases by
one:
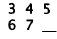
The missing number is 8, so the missing polygon is the one
with 8 sides.
44. Correct Response: B. Solving this problem involves using the
Pythagorean Theorem
twice.
The largest straight distance in the box is always a diagonal through the middle
of
the box. This diagonal forms the hypotenuse of a triangle whose side is the
edge,
and whose base is the diagonal of the bottom of the box.
To find the diagonal of the bottom of the box, we find the diagonal of a 2-foot
by 3-foot
rectangle using the pythagorean Theorem:
Diagonal of bottom of box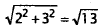 feet
feet
To find the length of the diagonal through the middle of the box we use the
Pythagorean Theorem again:
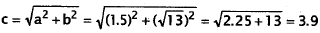 feet
feet
Choice A is the length of the diagonal in the bottom of
the box. Choice C results from
adding the lengths of the three sides of the box. Choice D results from not
taking the
square root of a 2 + b2.
45. Correct Response A. This is a multi-step problem in which you must
calculate each
contribution to the monthly cost of each apartment. For apartment A, rent is
$575 per
month. This apartment uses 250 kilowatt-hours of electricity, at 5G per
kilowatt-hour,
for a total of (250 kwh) x ($0.05/kwh) = $ 12.50. The total cost of commuting
from
apartment A is ($ 1 .50/day) x (30 days) = $45.00. Therefore, the total monthly
cost of
apartment A is $575.00 + $12.50 + $45.00 = $632.50. For apartment B, rent is
$600
per month; electricity is (225 kilowatt-hours/month) x ($0.05/kilowatt-hour) =
$11.25;
and commuting cost is ($0.75/day) x (30 days) = $22.50. Apartment B's total
monthly
cost is therefore $600.00 + $11.25 +22.50 = $633.75. Therefore, apartment A is
cheaper.
46. Correct Response: C. To solve this problem, you
must calculate the volume of each
tank, multiply by 3 for the three tanks to get the total capacity of the plant
in gallons,
and then multiply by 7.5 to get the total number of gallons.
For tank1 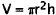 Volume of a
cylinder.
Volume of a
cylinder.
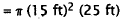 Substitute.
Substitute.
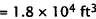
For 3 tanks,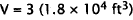
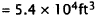
Each cubic foot contains approximately 7.5 gallons, so we
multiply to get the total
number of gallons:
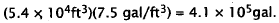
Choice A results from dividing by 7.5 instead of
multiplying. Choice B is the number of
gallons in one tank. Choice D results from incorrectly placing the decimal
point.
47, Correct Response: C. To solve this problem, you must calculate the
number of square
feet of surface area exposed to the air in all three tanks and multiply by the
amount of
water that evaporates per square foot per day.
Surface Area
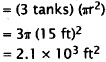
Number of gallons evaporating per day=
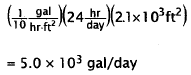
Choice A is the number of gallons evaporating per hour.
Choice B is the number of
gallons evaporating per day from one tank. Choice D results from incorrectly
placing
the decimal point.
48. Correct Response: D. This problem involves using the data in a table to
write an
equation that models the data. Since the depth is decreasing as time increases,
the
slope of this linear relation is negative. This eliminates choice C. When time
equals
zero, the depth is 25 feet. Substituting these values into the equations
eliminates A,
since the values do not make that equation true. At time equals I hour, the
depth is
I 7 feet. When we substitute these values into the equations, only equation D is
satisfied.



