Methods of Applied Mathematics Problem Set

Problem Set 5: Solutions

1. Use Lyapunov functions to describe the stability of the zero solution for each of the
following systems.

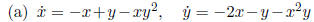This system looks like a stable linear node
with an additional damping term , so we look for a Lyapunov function to prove
stability. The most basic choice is a quadratic function ,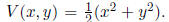
This function is clearly positive definite , has level sets which are closed orbits
around the origin, and is smooth. Thus, we can verify that

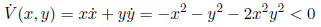
for (x, y) ≠ (0, 0). Thus, the origin is a global attractor.

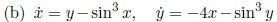This system looks quite similar to the previous
one - it is a a linear center plus a damping term. We would like the linear terms
to cancel when we compute 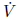, so we choose the quadratic function V (x, y) =
1/2(4x² + y²), which is positive de nite, has elliptical level sets around the origin,
and is smooth. Compute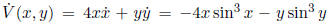This is
negative for x , y ∈(-π ,π ) - 0, so the origin is a local attractor.

2. We consider the system

Let us take the following Lyapunov function

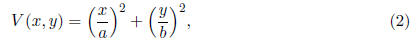
where a, b > 0. V (x, y) is clearly positive definite and its partial derivatives are all
continuous. Consider

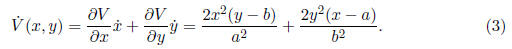
We need to show that 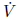(x, y) is negative definite in a neighborhood of (0, 0). In fact,
we will show that that 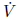(x, y) is negative definite inside the ellipse V (x, y) = 1. Take
any (x, y) ≠ (0, 0) satisfying

This necessarily implies |x| < a, |y| < b and consequently x - a < 0, y - b < 0, which
means 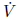(x, y) < 0. Note also that in region (??) we have 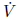(x, y) = 0  iff  x = 0, y = 0,
so 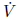(x, y) is negative definite there and all solutions starting in (??) approach the
origin

3. If (and only if) we choose A,B > 0, we have that V is C¹, positive definite, and,
since yf(y) > 0, defines closed orbits around the origin. Thus, to prove asymptotic
stability, we just need to show that 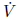< 0 in some neighborhood of the origin.

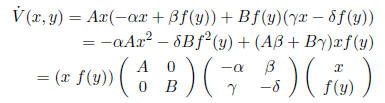
If we choose A = B = 1, the given condition that 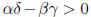(and, say, that α > 0 so
that the principal minors of the matrix are the correct signs ), we know that this is a
negative definite form and is thus negative for all nonzero (x, f(y)) (which correspond
to nonzero (x, y)).

4. The equation

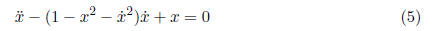
can be rewritten as a system

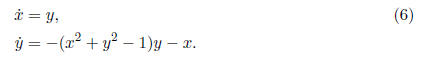
This is a Lienard equation (see Theorem 11.2, page 402, Jordan & Smith, 3rd edition).
We have f(x, y) = x² + y² - 1, g(x) = x, G(x) = 1/2x² and all the assumptions of the
theorem are satisfied. Define the energy function

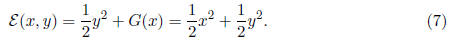
Note that E(0, 0) = 0, ε is positive definite, continuous and increases monotonically
in every radial direction from the origin. The family of contours of ε consists of circles
centered on the origin. Notice

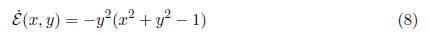
is positive semi-definite inside the circle x ² + y² = 1, so the critical point (0, 0) is
unstable. In fact, the linearization

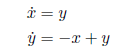
yields the eigenvalues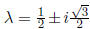 , which means the origin is an unstable spiral. Note
further that 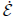is negative outside the mentioned circle, except at y = 0, and is zero
on the circle. This suggests that the circle x² + y² = 1 is the only closed curve in the
x, y plane that could potentially be a limit cycle. In fact, by direct substitution we
verify that

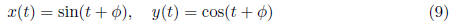
is the periodic solution of (??) (whose existence is asserted by Theorem 11.2). Given
the sign of 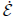in a neighborhood of the cycle, we conclude it is stable.