Matrix Operations I

1 Matrix operations

There are three basic matrix operations that would be part of any GPU
matrix toolkit:

1. The inner product of two vectors c = a · b.

2. Matrix-vector operations: y = Ax.

3. Matrix-Matrix operations: C = A + B, D = AB, E = A⁻¹.

A number of problems can be solved once one has these basic operations
(especially in physical simulations). This is one of the most studied problems
on the GPU.

2 The Inner Product

Consider the inner product c = a · b, which we rewrite as

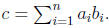
2.1 Technique 1: Small memory

Each vector is stored in a 1D texture. In the i^th rendering pass, we render a
single point at coordinates (0,0), having a single texture coordinate i . The
fragment program uses i to index into the two textures and returns the value
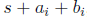, where s is the running sum maintained over the previous i − 1
passes. Note that since we cannot read and write the location where s is
stored in a single pass, we use a ping-pong trick to maintain s.

This procedure takes n passes, and requires only a fixed number of texture
locations (excluding the storage for a and b).

2.2 Technique 2: Fewer passes

The second technique uses more working memory (n units), but requires
fewer passes. We write a and b as 2D textures (2D textures allow for more
storage, since the dimension of a texture is typically bounded, and are better
optimized by the rasterizer).

We now multiply the contents of the textures, storing the result in a
third texture c. This can be done with a simple fragment program that takes
the fragment coordinates and looks up the a and b textures, returning their
product. We render a single quad in order to activate the fragment program.

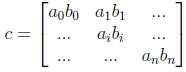
Finally, all the numbers in c must be summed together . This can be done
in log n passes , using a standard reduce operation.

This procedure takes only log n passes , but requires 3n units of texture
memory.

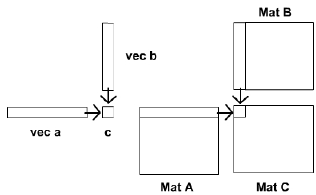
3 Matrix-Matrix operations

We can store matrices as 2D textures. Addition is trivial .

3.1 Multiplication

3.2 Technique 1: The Basic Approach

”Fast matrix multiplies using graphics hardware ” by Larsen and
McAllister”

Express multiplication of two matrices as dot product of vectors of matrix
rows and columns. That is to compute some cell c_ij of matrix C, we take the
dot product of row i of matrix A with column j of matrix B:

1st program used multitexturing and blending, each plane would compute
each place in the answer. In 1st pass: AB :

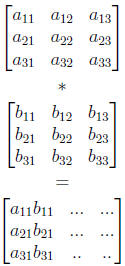
We can use inner quad idea to do this:

pass 1
if at location (x, y)
output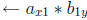
pass 2

output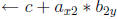
pass k
output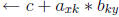



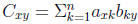
1)uses n passes
2)space N = n²

3.3 Technique 2: A Speedup

”Dense Matrix Multiplication” by
To make it faster:
Instead of making one computation per pass, compute multiple additions per
pass in fragment program:

Pass 1 becomes: output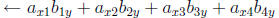
Must consider that there is a tradeoff between the length of fragment
program vs. the number of passes.

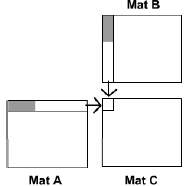
3.4 Technique 3: Using All Channels

”Cache and Bandwidth Aware Matrix Multiplication on the GPU”,
by Hall, Carr and Hart”.

We have been using only the red component, propose storing across all
colors:

divide into 2:

Basically a swizzle operation to speed things up.
Closing thought: The basic idea here is using the inner product calculation
in parellel.