Mathematics Practices
Exploration 15-4b: Limits and Curved Asymptotes
Objective: Analyze graphs of rational algebraic
functions with the help of synthetic
substitution and factoring.
|
1. Let 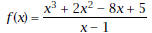
Plot the graph of f as
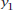 . Use a friendly window with . Use a friendly window with
an x-range of about 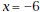 to to
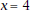 that includes that includes
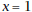
as a grid point. Have the grid off. Sketch the graph.
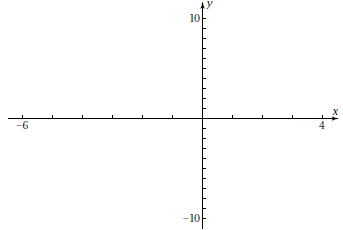
2.
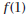 is undefined
because of division by zero . Trace is undefined
because of division by zero . Trace
to 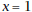 on your
graph. What feature does the graph on your
graph. What feature does the graph
have at this point? By tracing closer and closer to
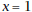 , find the
limit , find the
limit 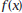 seems to be approaching as
seems to be approaching as
x approaches 1. Is the limit as x approaches 1 from
the left side the same as when x approaches 1 from
the right side?
3. Remove the discontinuity at
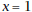 algebraically
by algebraically
by
factoring the numerator and reducing the fraction .
Evaluate the resulting quotient polynomial at
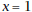
Is the answer equal to the limit you found in
Problem 2?
4. How do you read
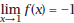 What does this What does this
equation mean ?
|
5. Let 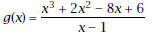
Plot the graph of g as
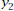 using “thick” style. What using “thick” style. What
feature does the graph of g have at
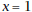 Sketch the Sketch the
graphs of 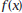 and and
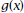 here, showing
their here, showing
their
relationship to each other.
6. Try to find 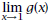 by tracing to x- values closer and
by tracing to x- values closer and
closer to 1. Try x-values on both sides of 1. What
happens to the quotient as x approaches 1?
7. To understand why the graph of
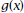 resembles resembles
the graph of 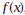 simplify the equation for
simplify the equation for
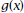
by synthetic substitution . Write the equation in
“mixed- number ” form as
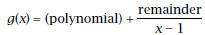
What relationship do you notice between the
equations for f (x) and g(x)?
|
8. Let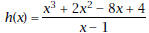
Plot the graph of
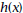 as as
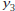 . .
9. The graphs of f and g from Problem 5 should look
like this . On this figure, sketch the graph of h.
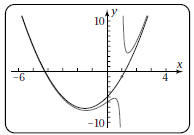
10. Simplify the equation for
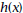 by long
division or by long
division or
synthetic substitution. Write the result in mixed-number
form as 
|
11. How is the polynomial part of
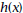 in Problem 10 in Problem 10
related to the graph of
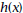 ? ?
12. Why is it important for your work to be 100% correct
in problems like these that are sequential?
13. Write a paragraph summarizing the things you
have
learned about rational functions, removable
discontinuities, asymptotes, etc. as a result of doing
this Exploration. |
Exploration 15-5a: Rate of Change Date :
of a Polynomial Function
Objective: Find the instantaneous rate of change of
a polynomial function at a given
value of x.
Astronaut Spencer Spacey takes off from the planet
Alderaan. He starts his rocket countdown at time
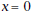 minutes. Shortly thereafter his
spaceship takes off. minutes. Shortly thereafter his
spaceship takes off.
It rises for a while, then drops while his second-stage
rocket engine is starting up, and then rises again.
Spencer’s computer finds that his distance,
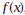 miles, miles,
above the surface is given by
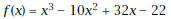
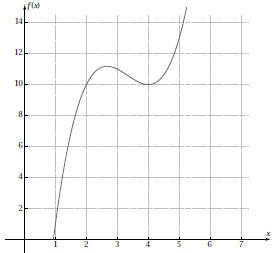
1. How far is Spencer from the surface at
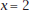 min? at min? at
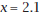 min? How far did he go in this time
interval? min? How far did he go in this time
interval?
What was his average velocity for this time interval?
2. What is Spencer’s average velocity for the time
interval from 2 minutes to x = 2.001 minutes?
|
3. Spencer’s instantaneous velocity at 2 minutes is the
limit of his average velocity between 2 and x minutes
as x approaches 2. From your answers to Problems 1
and 2, what do you conjecture that his instantaneous
velocity equals at 2 minutes?4. Between
time 2 and x minutes, Spencer travels
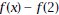 miles. So his average rate miles. So his average rate
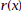 is is
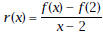
Substitute for
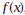 and and
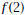 and simplify the and simplify the
numerator. Then use synthetic substitution to do the
division, thus removing the discontinuity at
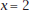
Write a simplified equation for 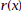 . .
5. Use this simplified equation for 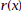 to find the limit
to find the limit
as x approaches 2. Does this confirm the
instantaneous velocity you found in Problem 3?
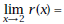
6. Plot a line through the point 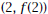 that has a slope
that has a slope
equal to the instantaneous velocity you found in
Problem 5. Take into account that the two axes have
different scales. How does the line relate to the
graph?
Relationship: 
|
7. Find Spencer’s instantaneous velocity at time
3 minutes by starting with
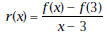
Explain the fact that the answer is negative .
8. Let 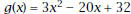 . Find . Find
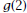 and and
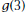 . How do . How do
your answers compare with the instantaneous
velocities at times
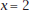 and and
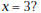
9. There is an algebraic way to find the instantaneous
rate of change of a polynomial function. Suppose
that 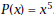 If If
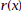 is the
average rate of change is the
average rate of change
between the fixed time c and the variable time x,
then 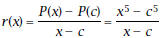
Divide by means of synthetic substitution. Write a
polynomial equation for
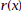 . (It will
involve the . (It will
involve the
constant c.)
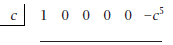
10. By appropriate calculations, show that
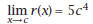
|
11. Explain how you can get the 5 and the 4 in
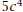 from from
the original polynomial 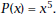
12. Suppose that 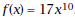 What do you think
would What do you think
would
be an equation for the function
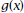 that gives
the that gives
the
instantaneous velocity of
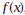 ? ?
13. Show that you can use the patterns you found in
Problems 11 and 12 on the function
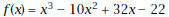
to get the velocity function from Problem 8,
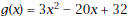
14. Look in Section 15-5 to find the special name given
to the velocity function.
15. What did you learn as a result of doing this
Exploration that you did not know before?
|
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
May 8th
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
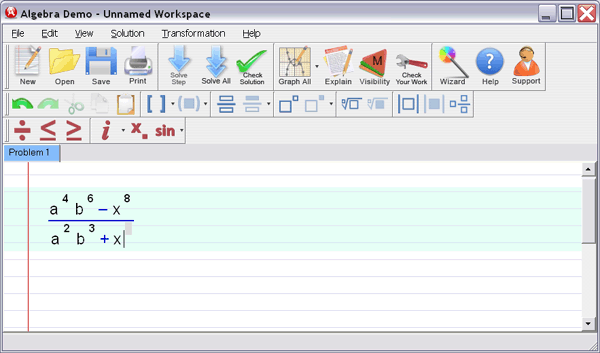
Step 2 :
Let Algebra Helper solve it:
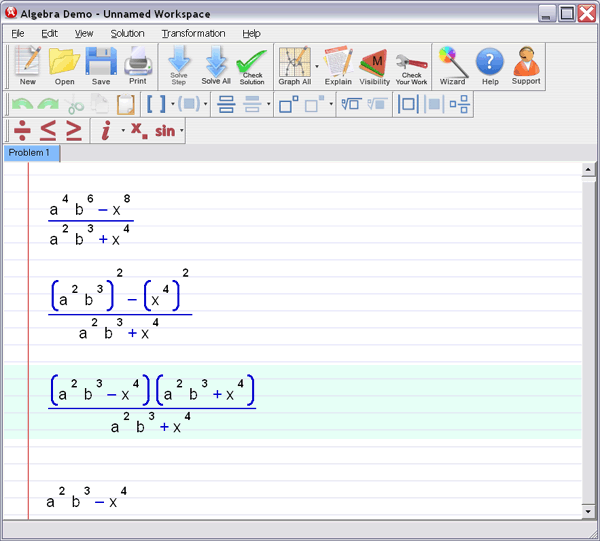
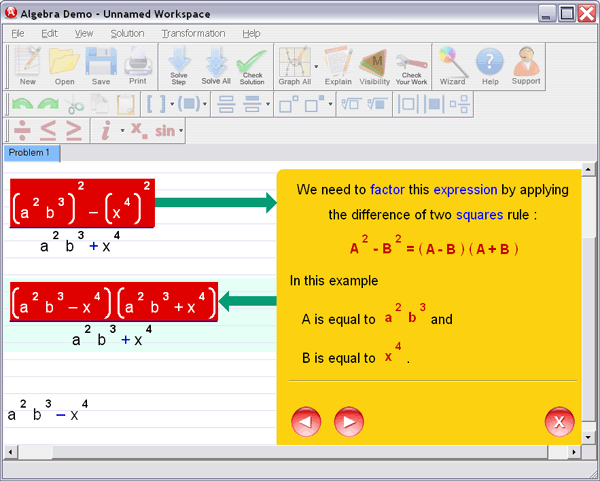
Step 3 : Ask for an explanation for the steps you don't understand:
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



