How well do you know
mathematics for teaching ?
Overview: Trying your hand at
using mathematics in teaching
1. Noticing and identifying the mathematics
in students’ productions
2. Posing strategic mathematical questions
to students
3. Composing usable and precise
mathematical definitions
4. Writing a quiz and choosing examples
Case 1:
Noticing and identifying the
mathematics in students’
productions
Classroom Context
• Third graders (ages 8 - 10)
• Mathematics: even and odd
numbers, definitions, showing why
something is true
• Multi-lingual and multi-cultural class
What do you hear and
notice mathematically?
• What is going on mathematically?
• What definitions of even and odd do
you hear (implicit) in children’s talk?
Case 2:
Posing mathematical
questions to students
What would be good to ask
Shea?
“What about the number ____?”
Case 3:
Composing usable and precise
mathematical definitions
What makes a “good”
definition?
• Mathematically precise –– correctly
identifies the kind of object, process,
property
• Usable by user community –– based on
already-defined and understood term
• Good for growth: Will expand easily as
students advance
What is a mathematically
precise and usable definition
of “even number”
for third graders? |
Proposed definitions for
even numbers
1. An even number is a number that can be divided into two
equal parts.
2. An even number is any multiple of 2.
3. An even number is any integer multiple of 2.
4. An even number is any number whose unit digit is 0, 2,
4, 6,
or 8.
5. An even number is a whole number with zero remainder
when
divided by 2.
6. A whole number is even if it is the sum of a whole
number
with itself.
Consequences
a) An even number is a number that can be divided into two
equal parts.
b) An even number is any multiple of 2.
All numbers, for example 7, 3/5, √2, π, are even!
c) An even number is any integer multiple of 2.
This is a correct definition of even number, but not usable by third
graders.
d) An even number is any number whose unit digit is 0, 2,
4, 6, or 8.
In this case, 36.7 is an even number!
e) An even number is a whole number with zero remainder
when divided by 2.
According to this, -6 is not even.
f) A whole number is even if it is the sum of a particular
whole number with itself.
This is a correct definition of evenness for whole numbers, and is
consistent with the general definition for integers that students will
learn later.
Case 4:
Writing a quiz and choosing
examples
Designing a quiz on even and
odd numbers for Shea and his
classmates
• Choose a list of numbers that you would
like Shea and his classmates to classify
correctly so that you can learn whether
they understand what makes a number
even or odd
– Does it matter what numbers you pose? Why or
why not?
Opportunity:
Study of Instructional Improvement
• Study of three Comprehensive School
Reforms; teacher knowledge a key variable
• Instrument development goals:
– Usable with 5000 teachers: survey, multiple
choice
– Measure content knowledge teachers use in
teaching – not just what they know
– Differentiate among teachers
– Non-partisan
Overarching findings:
Factor analyses
• Multidimensionality of mathematical knowledge
for teaching
– Knowledge of students and content different from
“pure” content knowledge
– Knowledge differentiable by topic domain (e.g.,
algebra , geometry)
– Number and and operations mathematical knowledge
for teaching
• Specialized
• Common
• Tentative conclusion: existence of a kind of
“professional” knowledge for teaching
Validating our measures
How do we interpret teachers’ performance on our
questions?
1. Their score reflects their mathematical thinking
– Cognitive interviews
2. Higher scores mean higher-quality mathematics
instruction
– Videotape validation study
3. Scores reflect common and specialized knowledge of
content
– Mathematician and non-teacher interviews
4. Higher scores related to improved student learning
– Study of Instructional Improvement student gains
analysis
Percentage of mathematicians
answering each survey item correctly
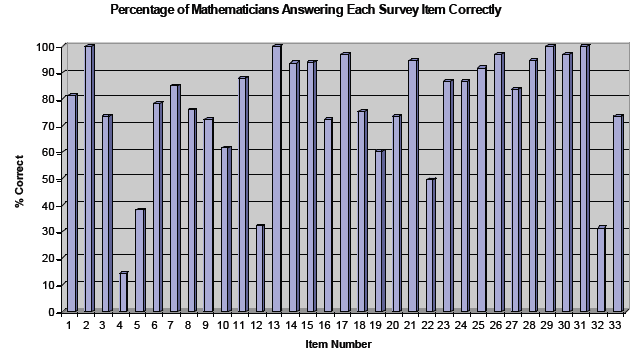
Why did mathematicians get
items wrong?
• Items had mathematical flaws.
• Items required knowledge of learners.
• Items demanded mathematical knowledge
unique to the work of teaching:
– Making sense of non-standard solutions or
ideas
– Choosing numerical examples
– Choosing representations
Which student is using a method that
would work for any two whole numbers?
| Student A |
Student B |
Student C |
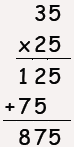 |
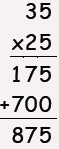 |
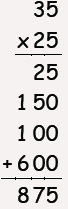 |
Modeling multiplication
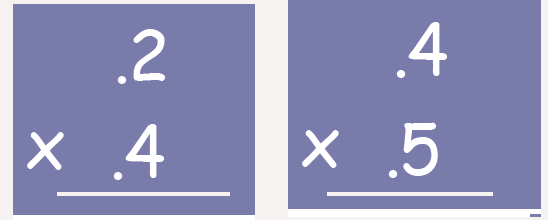
Model each problem using an area
interpretation and a repeated addition
interpretation of multiplication, matching
each part of the problem to the drawing .
Linking teacher knowledge and
student achievement
• Questionnaire consisting of 30 items (scale reliability
.88)
• Model: Student Terra Nova gains predicted by:
– Student descriptors (family SES, absence rate)
– Teacher characteristics (math methods/content, content
knowledge)
• Teacher content knowledge significant
– Small effect (< 1/10 standard deviation): 2 - 3 weeks of
instruction
– But student SES is also about the same size effect on
achievement
(Hill,Rowan, and Ball, AERJ, 2005)
Conclusions
1. Content knowledge is crucial to teaching
effectiveness.
2. The mathematical knowledge for teaching
needed is specialized and is more than common
content knowledge known by any well-educated
adult.
3. This kind of content knowledge in mathematics
can be assessed.
4. This is a professionally-shaped way of knowing
the subject. Who knows this content, and who
can teach it to teachers?



