MATH STUDY GUIDE
To the students:
When you study Algebra, the material is presented to you in a logical
sequence. Many ideas are developed, left, and then returned to when your
knowledge is broader. Many different kinds of problems have similar
instructions. This presents great difficulty when trying to prepare for a final
exam or keep up in the next Math class . You have mastered all the skills, but
which one do you use in a specific problem? This guide was written to help you
to re-organize your knowledge into a more usable form.
When you are faced with a problem that begins, “ Solve for x .” What should you
do? As you will see, there are at least 9 different situations where you have
seen that instruction. This guide will give you the key questions to ask
yourself in order to decide what procedure to use. The main steps that are
involved are included. The questions are asked in the ORDER that you should ask
them. Each is referenced with a section number (or if only part of the section
is involved, the specific page or problem number is given.)
To use this guide effectively, you should first read through the guide. Each
reference to a section should be examined carefully. Can you make up a problem
like the one being described? Would you know how to solve that problem without
any clues? Look at the problem or section referenced. Is it like yours? Can you
work those easily? If so, go on to the next topic. If not, highlight that line
with a marker for further study. Perhaps you should put an example problem on a
3 by 5 card (include the page number) for practice later. Now read the section
again carefully. Work the examples and select a few similar problems from the
exercises (odd ones so you can check the answers) for practice. When you finish
a whole type (i.e. Solve for x) mix your 3 by 5 cards and treat them like a
test. Any that you miss will direct you back to the sections where you need
further study.
If you need further help, consider asking for a tutoring appointment in the
Math Lab. When you know what SPECIFIC topics present a problem for you, you can
make a tutoring session much more effective and be of help so your tutor can
know what help you need. See the Math Lab Coordinator early in the semester to
fill out a tutoring application.
SOLVE FOR X
Is there more than one letter?
- Treat all letters EXCEPT the one you are solving for as if they were
numbers. |
Sec. 2.4 |
Is there a variable under a radical?
- Solve for the radical first , then square both sides of the equation
and simplify. You MUST check the solutions because some may not check in
the original. |
Sec. 9.5 |
Are there one or more fractions in the equation ?
- Multiply both sides of the equation by the denominator (or LCD.)
Always be sure that no denominator can be zero . |
Sec. 8.6 |
Is there an x3 or higher power of x?
- The only way we could work this would be to gather all terms on one
side of the equation and then factor.
- Use the Zero Product Principle to set each factor equal to zero, and
then solve. There might be as many solutions as the highest power of x . |
|
Is x2 the highest power of
x? Use any of the following:
1) Try factoring, it sometimes works
|
Sec. 7.6
|
| 2) Complete the square. WARNING: If a
perfect square equals a negative number, quit. There is no real
solution. |
Sec 10.2 |
3) Put the equation in standard form
and apply the Quadratic Formula.
a) Simplify the radical, if possible.
b) If the radical contains a perfect square, rewrite the solution twice,
once with a + and once with a -, then simplify further.
c) If the radical contains a negative number there is no real solution. |
Sec. 10.3 |
Are there only x terms and constants?
1) Remove parentheses using the Distributive Law and simplify both
sides. If you now find an x2 term, see instruction above.
2) Using the Addition Property of Equality, gather the x terms on one
side of the equation.
3) Using the Addition Property of Equality, gather the constants on the
other side.
4) Divide both sides of the equation by the coefficient of x . |
Sec. 2.1-2.3 |
5) If the x terms disappear and:
a) You get nonsense such as 5 = 2, then there is NO SOLUTION.
b) You get a true statement such as 6 = 6, then ANY NUMBER is a
solution. (This is called an identity). |
Sec. 2.3 |
Is this an inequality?
- Treat it as an equation except that when you multiply or divide by a
negative you must REVERSE the inequality. Graph the solution . |
Sec. 2.6 |
SOLVE FOR X AND Y
| To solve 2 equations in 2 unknowns
there are 2 (equally good) methods. Each eliminates one variable in the
first step. |
|
| 1) Substitution |
Sec. 5.2 |
| 2) Addition Method |
Sec. 5.3 |
(You can observe the approximate
solution by graphing both equations on the same graph. The solution is
the coordinates of the point where the lines intersect.)
What can ‘go wrong?’
a) You lose BOTH variables in the first step and end up with nonsense
like 0 = 7. There is NO SOLUTION. (In this case the lines on the graph
would be parallel, so they don’t meet at all.)
b) You lose both variables in the first step and end up with truth like
0 = 0. The answer is that there are MANY SOLUTIONS. (In this case if you
graphed the lines, one would be superimposed over the other. Both
equations describe the same line so any point on the line represents a
solution.) |
Sec. 5.1 |
COMPUTE OR EVALUATE
| Arithmetic, Signed Numbers and Absolute Value
Order of Operations
1) Work from the innermost grouping out.
a) The numerator and denominator of a fraction are each groupings
b) If the fraction is complex, find SOME part that can be simplified and
start there or use identity of 1.
2) Within a group:
a) Exponentiate first. (SEE Exponential Expressions for more detail .)
i) Only the closest possible base is raised to the power. To raise a
negative base or a fractional base to a power REQUIRES parentheses
ii) Any base to the zero power is 1. Any base to a negative power
indicates that you take the reciprocal.
b) Multiply and divide, moving from left to right.
c) Simplify signs, if necessary.
d) Algebraic addition is last |
Sec. 1.8 |
GRAPH
To graph ANY equation involving x and
y:
1) Make a table for x and y.
2) Pick at least 5 values, some negative, for x. (Occasionally, it may
be convenient to pick some values for y.)
3) Using the formula given to you, complete the table. (Substitute each
value into the formula then compute the remaining value.)
4) Plot the points from your table on the graph.
5) Connect the points smoothly moving from left to right. |
Sec. 4.1 |
| To graph an equation like x = 4 (or
any number.) All x values are 4, pick anything at all for y. The result
will be a vertical line. |
Sec. 4.2 |
| To graph an equation like
y = 7 (or any number.) All y values are 7, pick anything at all for x.
The result will be a horizontal line. |
Sec. 4.2 |
To graph an INEQUALITY:
1) Graph as above but dot in line or curve.
2) Pick any point well away from the dotted edge. (If the origin
qualifies, it is an easy choice.)
3) Substitute the coordinates of your point into the inequality.
a) If the test point makes the inequality true, shade in that side of
your graph.
b) If the test point does NOT make the inequality true, shade in the
other side.
4) If the inequality allows =, (either ≥ or ≤) fill in the edge of the
graph border solidly. |
Sec. 4.6, 5.5 |
| The x-intercept of a line or curve is
where it crosses the x-axis. To find its value, substitute 0 for y. |
Sec. 4.2 |
| The y-intercept is where the line or
curve crosses the y-axis. To find its value, substitute 0 for x. |
Sec. 4.2 |
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
April 25th
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
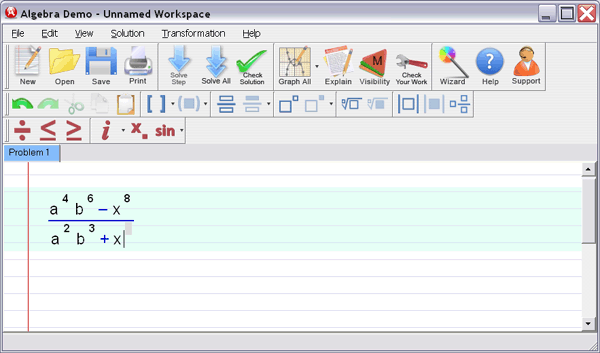
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
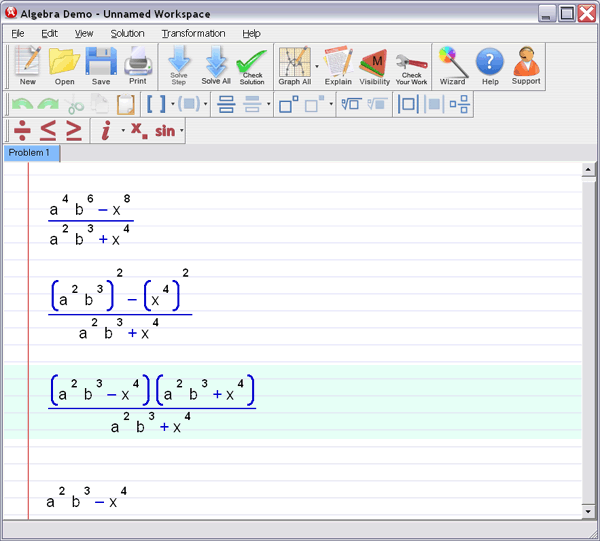
Step 2 :
Let Algebra Helper solve it:
Step 3 : Ask for an explanation for the steps you don't understand:
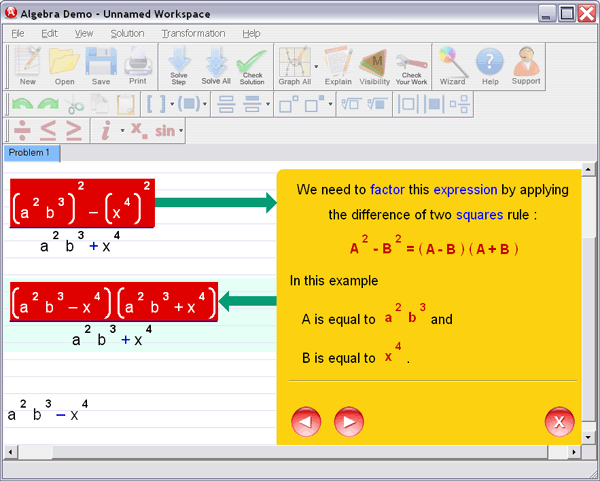
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



