1. To accompany the HW due on Jan. 29
1. (a) Use the DeMorgan laws to argue that 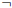 (A
and
(A
and 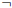 B) ≡ (
B) ≡ (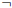 A
or B).
A
or B).
(b) Use induction to show n! ≤ nn for every n ∈ N.
2. (a) Use the DeMorgan laws to argue that 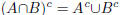 and
and 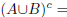
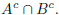
(b) Prove that the empty set is a subset of every set.
3. Interpret in words: 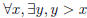 but not
but not
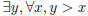 . (x, y are integers)
. (x, y are integers)
4. (a) Prove that 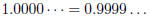 using the geometric series
formula :
using the geometric series
formula :
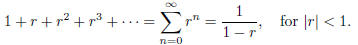
Hint: use 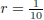 .
.
(b) Briefly explain why (1+b)2 > 1+2b in the proof of the Thm. in
§1.4.1.
(c) Briefly explain why the conclusion of the proof of Thm. in §1.5.2
follows from the Archimedean Property of R .
2. To accompany the HW due on Feb.7
1. Prove n!≤nn for every n ∈ N, without using induction.
2. (a) Prove that 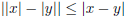 for x, y ∈ R.
for x, y ∈ R.
(b) Prove 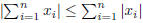 for
for
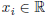 .
.
3. Show that if r is a nonzero rational number and x ∈ R \ Q (i.e., x is
irrational), then r + x and rx are both irrational.
3. To accompany the HW due on Feb.14
The first two problems use these two definitions.
Definition 1. A dyadic rational is a rational
number of the form
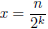 , n ∈ Z, k = 0, 1, 2, ...
, n ∈ Z, k = 0, 1, 2, ...
So, for example, 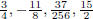 are all dyadic rationals .
are all dyadic rationals .
Definition 2. For A 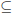 B
B 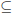 R, we say A is dense
in B iff between any two points
R, we say A is dense
in B iff between any two points
of B we can find a point of A, i.e.,
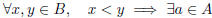 with x < a < y.
with x < a < y.
For example, we've seen that Q is dense in R. It is important that all
inequalities
are strict in this definition.
1. Show that the dyadic rationals are dense in Q.
2. Show that density is transitive, i.e., that if A is dense in B and B is dense
in C, then A is dense in C. (Hint: in this situation, A 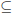 B
B 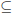 C
C 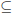 R.)
R.)
Deduce that the dyadic rationals are dense in R.
3. Show that log n is increasing , using nothing but the fact that log x > 0 for
x > 1.
4. Show that  .
.
4. To accompany the HW due on Feb. 21
1. 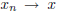 iff every neighbourhood of x of the form
iff every neighbourhood of x of the form
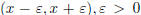 ,
,
contains all but finitely many points 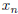 .
.
2. Can you have a sequence 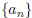 which, for any given rational number p ∈ Q
which, for any given rational number p ∈ Q
has a subsequence 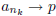 ? Construct one or prove it is impossible.
? Construct one or prove it is impossible.
3. Prove the equivalence of the two definitions of Cauchy sequence.
4. If 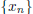 is Cauchy in R and some subsequence
is Cauchy in R and some subsequence
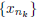 converges to x ∈ R,
converges to x ∈ R,
then prove the full sequence 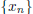 also converges to x.
also converges to x.
5. To accompany the HW due on Feb. 28
No extra problems this week.
6. To accompany the HW due on Mar. 7
(1) If 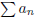 converges and
converges and
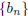 is monotonic and bounded, then
is monotonic and bounded, then
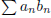 con-
con-
verges.
(2) Give an example to show that you can have 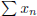 diverge and
diverge and
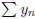 diverge,
diverge,
but 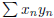 converges.
converges.
(3) (a) Show that if 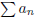 converges absolutely, then
converges absolutely, then
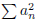 does, too. Is this
does, too. Is this
true without the hypothesis of absolute convergence?
(b) If 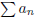 converges and
converges and
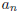 ≥ 0, what can be said about
≥ 0, what can be said about
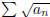 ?
?
(4) (a) (Dirichlet's Test) Suppose that the partial sums
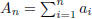 form a
form a
bounded sequence, and suppose there is a sequence
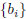 with
with 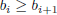
and 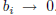 . Then show
. Then show
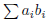 converges. (Hint:
converges. (Hint:
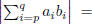
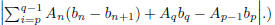
(b) Use Dirichlet's test to prove the alternating series test.
(5) For an alternating series, 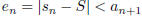 , where
, where
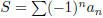 .
.
7. To accompany the HW due on Mar. 14
(1) Define 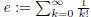 . Prove
. Prove
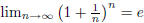 .
.
(2) For how many points x ∈R can a power series converge conditionally?
Prove it.
8. To accompany the HW due on Mar. 28
(1) An even function times an even function is even. An odd function times an
even function is odd. What about an odd function times an odd function?
( Compare with the rules for integers.)
(2) If f and g are bounded on I, show that f + g and fg are bounded on I.
(3) Show that if 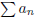 converges absolutely, then so does
converges absolutely, then so does
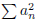 . Is this true
. Is this true
without the hypothesis of absolute convergence?
(4) Does 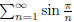 converge?
converge?
9. To accompany the HW due on Apr. 4
(1) 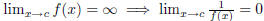 .
.
(2) (Pasting Lemma) Let f be continuous on [a, b] and g be continuous on [b, c].
If f(b) = g(b), then
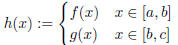
is continuous on [a, c].



