1. Determine whether each of the following
relations is a function, and justify your
answer.
(a) {(-1, 1), (2, 5), (3, 5) }
Is a function because no first member of a pair is associated with more
than one second member.
(b) {(-1, 1), (2, 5), (2, 3) }
Is not a function because 2 is a first member in the set of ordered pairs ,
and two second members, 5 and 3, are associated with 2.
2. For each of the following equations, determine whether the equation
defines y
as a function of x
(a) y = x2
Is a function because given x, there is only one way to form its square,
y = x2.
(b) x = y2
Is not a function because a value of x does not uniquely determine a y
that satisfies x = y2. For example, x = 1 has two value of y associated with
it: y = ±1.
(c) y + 2 = |x|
This is just y = |x| − 2. Each value of x uniquely determines a value y
satisfying y = |x| − 2.
3. Let f(x) = x2 − 2x. Find the difference quotient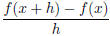
.
Note that f(x + h) = (x + h)2 − 2(x + h). The difference quotient is
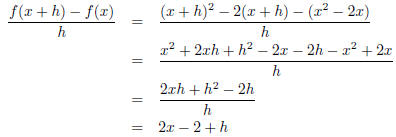
4. Consider the function
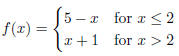
Make a table listing some of the ordered pairs in the function, sketch the
graph,
and state its domain and range. Make sure you indicate which set is the domain
and which set is the range.
5. State the domain and range of the function described by the equation
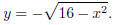
To determine the domain, we insist that 16 − x2 ≥ 0 because we cannot take the
square root of a negative number . Thus x2 ≤ 16, which means that −4
≤x≤ 4,
so the domain is [−4, 4].
Observe as x varies through the domain, x2 varies from 0 to 16 and
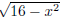varies
from 4 to 0. Thus the range is [−4, 0].
6. Write the equation of each graph after the indicated transformation.
(a) The graph of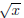 
is translated 5 units to the left.
(b) The graph of y = x2 is translated 10 units to the right and 4 units upward.
y = (x − 10)2 + 4
(c) The graph of y = |x| is reflected in the x-axis, stretched by a factor of 3,
and then translated 7 units to the right and 9 units upward.
y = −3|x − 7| + 9
7. Detemine algebraically whether each function is even, odd, or neither. In
each
case, justify your answer.
A function f is even if f(−x) = f(x), and is odd if f(−x) = −f(x).
(a) f(x) = x4 − 2x2
Notice that
f(−x) = (−x)4 − 2(−x)2 = x4 − 2x2
f(x) = x4 − 2x2
so this function is even.
(b) f(x) = −x
Notice that
f(−x) = −(−x) = x
−f(x) = −(−x) = x
So this means that the function is odd.
(c) f(x) = (x − 1)2
This function is neither odd nor even. To see why, observe that
f(−x) = (−x − 1)2 = ((−1)(x + 1))2 = (−1)2(x + 1)2 = (x + 1)2.
Therefore
f(−x) = (x + 1)2.
This is clearly not the same as
f(x) = (x − 1)2
(plug in 2 for x to see that they are different) so the function is not even.
Similarly, f(−x) is not the same as
−f(x) = −(x − 1)2
(plug in 0 for x to see that they are different) so the function is not odd.
Therefore, it is neither.
8. Solve each inequality by graphing an appropriate function, and state the
solution
set using interval notation. Here are the inequalities.
(1) (x − 1)2 − 9 < 0
(2) (x − 1)2 − 9 0
The appropriate function is f(x) = (x−1)2 −9 I won’t sketch the graph, but I
will
describe it in sufficient detail to enable you to graph it. The graph is a
parabola
that opens up and has its vertex at (1, -9). Its y-intercept is f(0) = 1 − 9 =
−8.
To find its x- intercepts , solve the equation
(x − 1)2 = 9
x − 1 = ±3
so x = −2 or x = 4.
Put your solutions in interval notation here:
(1) (x − 1)2 − 9 < 0
(2) (x − 1)2 − 9 ≥0
9. Let f(x) = 3x − 1 and g(x) = x2 + 1. Evaluate the
expression (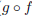
)(x).
(
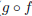)(x) = g(f(x)) = g(3x − 1) = (3x − 1)2 + 1 = 9x2 − 6x + 1 + 1.
10. Let f(x) = |x|, let g(x) = x−7, and let h(x) = x2. Write each of the
following
functions as a composition of functions chosen from f, g, and h.
(a) P(x) = |x − 14| − 7
This function subtracts x from its argument twice (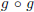
), takes the
absolute value (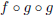
) and then subtracts 7 again (
)
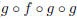(b) N(x) = (|x| − 7)2
This function takes the absolute value of its argument (f), substracts 7
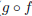() and then squares (
).
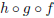11. Find the inverses of the following functions:
(a) f(x) = 2x + 5
This is simple enough that we can find the inverse mentally. Function f
(1) multiplies its input by 2
(2) adds 5 to the result
The inverse function will reverse these actions as follows
(1) subtract 5 from its input
(2) divide the result by 2
Clearly the inverse function is the function
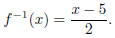
(b)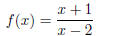 
Write
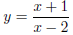
and use the switch and solve method . After switching, solve for y as
follows:
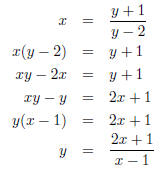
12. Show that the function given by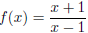 
is one-to-one.
To do this we need to show that
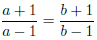
implies that a = b.
Simplify the equation as follows :
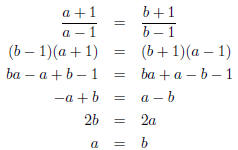
13. Show that the function given by y = |x + 2| is not one-to-one.
We need to show that there are two different values x = a and x = b such that
|a + 2| = |b + 2|.
We can think of such values by contemplating the meaning of an absolute value.
Now |x+2| stands for the distance of x from -2. We need to find different
numbers
that are the same distance away from -2. To do this, imagine -2 on the number
line , and take one step to the right arriving at -1, or one step to the left,
arriving
at -3. Note that
| − 1 + 2| = | − 3 + 2|
