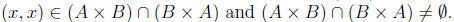Math 111 Practice Midterm II Solutions

For each problem, prove the statement. Indicate what type of proof (trivial, vacuous, direct, by
contrapositive, or by contradiction) you are using.

1. Let x be a real number .

(a) If x >-7, then -5-x^2 < 0.

For any real number x , x≥0. Therefore -x^2≤0, and-5-x^2 ≤-5 + 0 = -5 < 0.
(This is a trivial proof.)

(b) If |x| = 5, then x^2 + x + 1 > 20.

If  |x| = 5, then either x = 5 or x = -5. Thus we can consider the following two
cases:

Case 1. x = 5.

Then x^2 + x + 1 = 5^2 + 5 + 1 = 31 > 20.

Case 2. x = -5.

Then x^2 +x+1 = (-5)^2 +(-5)+1 = 21 > 20. (This is a direct proof by cases.)

(c) If 2x > x^2 + x^3, then x < 1.

We will prove this statement by contrapositive. Suppose x≥1. Then x^2≥x and
x^3≥x. Adding these two inequalities gives x^2 + x^3≥2x; thus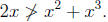

2. Let n and m be integers.

(a) If 3n^2 + 5n is odd, then n≥10.

We will show that for any integer n, the number 3n^2 +5n is even. To do this, we will
consider two cases :

Case 1. n is even.

Then n = 2k for some k ∈ Z. Therefore 3n^2+5n = 3(2k)^2+5(2k) = 12k^2+10k =
2(6k^2 + 5k). Since 6k^2 + 5k ∈ Z, the number 3n^2 + 5n is even.

Case 2. n is odd.

Then n = 2k + 1 for some k ∈ Z, and 3n^2 + 5n = 3(2k + 1)^2 + 5(2k + 1) =
12k^2+12k+3+10k+5 = 12k^2+22k+8 = 2(6k^2+11k+4). Since 6k^2+11k+4 ∈ Z,
the number 3n^2 + 5niseven.

Since 3n^2 + 5n is never odd, the implication follows. (This is a vacuous proof.)

(b) If n is even, then 3n^2-2n -5 is odd.

Suppose n is even. Then n = 2k for some k ∈Z. Therefore

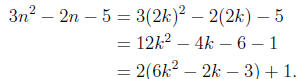
Since 6k^2-2k-3 ∈ Z, the number 3n^2-2n-5 is odd. (This is a direct proof.)

(c) If 7n^2 + 4 is even, then n is even.

We will prove this statement by contrapositive. Suppose n is odd. Then n = 2k + 1
for some k ∈ Z. Therefore 7n^2 + 4 = 7(2k + 1)^2 + 4 = 7(4k^2 + 4k + 1) + 4 =
28k^2 +28k +11 = 2(14k^2 +14k +5)+1. Since 14k^2 +14k +5 ∈ Z, 7n^2 +4 is odd.

(d) If n-5m is odd, then n and m are of opposite parity.

We will prove the statement by contrapositive. Thus we will prove that if n and m
are of the same parity, then n-5m is even.

Case 1. n and m are both even.

Then n = 2k and m = 2l for some k,l ∈ Z. Therefore n-5m = 2k-5(2l) =
2k-10l = 2(k-5l). Since k-5l ∈ Z, the number n -5m is even.

Case 1. n and m are both odd.

Then n = 2k + 1 and m = 2l + 1 for some k,l ∈ Z. Then n -5m = 2k + 1 -
5(2l +1) = 2k +1-10l-5 = 2k-10l-4 = 2(k-5l-2). Since k-5l-2 ∈ Z,
the number n -5m is even.

(e) If 5 | (n-1), then 5 | (n^3 + n-2).

Suppose 5 | (n-1). Then 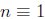(mod 5). Therefore 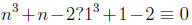(mod 5).
This implies that 5 | (n^3 + n-2). (This is a direct proof.)

Another proof: Suppose 5 | (n-1). Then n-1 = 5k for some k ∈ Z. Therefore
n = 5k+1, and we have n^3 +n-2 = (5k+1)^3 +(5k+1)-2 = 125k^3 +75k2 +15k+
1+5k+1-2 = 125k^3+75k^2+20k = 5(25k^3+15k^2+4k). Since 25k^3+15k^2+4k ∈ Z,
we have 5 | n^3 + n-2. (This is also a direct proof.)

(f) 3 | mn if and only if 3 | m or 3 | n

We have two implications to prove.

-> Suppose 3 | mn. Show that 3 | m or 3 | n.
We will prove this statement by contrapositive. Suppose 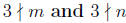. Then
m = 3k + c and n = 3l + d for some k, l, c, d ∈ Z where c and d are equal to
either 1 or 2. We have

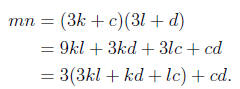
Case 1. c = d = 1

Then cd = 1, and mn = 3(3kl + k + l) + 1. Thus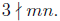

Case 2. WLOG c = 2, d = 1.

Then cd = 2, and mn = 3(3kl + 2k + l) + 2. Thus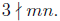

Case 3. c = d = 2

Then cd = 4, and mn = 3(3kl+2k +2l)+4 = 3(3kl+2k +2l+1)+1. Thus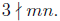

<-Suppose 3 | m or 3 | n. Show that 3 | mn.

We will prove this statement directly. Without loss of generality, suppose 3 | m.
Then m = 3k for some k ∈ Z. Therefore mn = 3kn is divisible by 3.

3. The number log ₃2 is irrational.

Suppose log ₃2 is rational. Then log₃2 = m/n for some m,n ∈ Z, n > 0. Therefore 3^m/n = 2,
so 3^m = 2ⁿ. Since n > 0, 3^m = 2ⁿ > 1. We know that 3^m is odd since it is a product
of odd integers (or you can prove a little lemma here that says, If a is odd and m is a
positive integer , then a^m is odd.). But we also know that 2ⁿ is even since it is a product
of even integers (or you can prove another similar lemma if you are not convinced). This
is a contradiction, since an odd number cannot be equal to an even number. Therefore
log ₃2 is irrational. (This is a proof by contradiction.)

4. The product of a nonzero rational number and an irrational number is irrational.

Suppose there exist a nonzero rational number x and an irrational number y such that xy
is rational . Then x = k/l for some k,l ∈ Z, k, l ≠ 0 and xy = m/n for some m, n ∈Z, m≠0

We have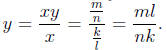Since ml,nk ∈Z and nk ≠ 0, y is rational . Contradiction.
(This is a proof by contradiction.)

5. Let A and B be sets. Then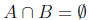if and only if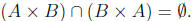

We have two implications to prove.

-> Suppose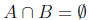Show that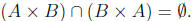

We will prove this statement by contrapositive. Suppose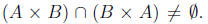

Then there exists an element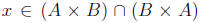Therefore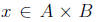and

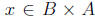Thus x = (y, z) for some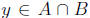(and 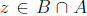It follows that)

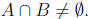
<-Suppose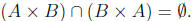Show that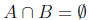

We will prove this statement by contrapositive as well. Suppose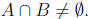Then
there exists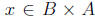Since x ∈ A and x ∈ B, we have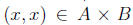and

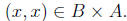Thus