A linear function ,f of x, can be written in the
form f(x)=ax+b, where a and b are real numbers. The graph of a linear function
is a nonvertical linea with slope a and y-intercept (0,b)
Problem Type #1: Consider the following linear
function. Reduce all fractions to lowest terms.
1) Find the slope and y -intercept (entered as an ordered
pair ) of the line which is represented by this function.
2) Graph this linear function by finding two points on the
line. (Note: You can use the y-intercept as one of the points.)
EX1:
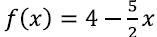
EX2:
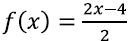
EX3:
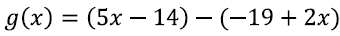
A quadratic function ,f of x, can be written in the
form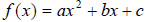 
where a, b, and c are real numbers and
a ≠0. The graph of a quadratic function is a parabola.
The vertex form of a quadratic function is
.
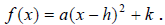(Vertex form can be arrived at by completing the square or by using the
Vertex Formula .)
The graph of f is a parabola with vertex
(h,k) and axis of symmetryhx x=h
The parabola opens up a>0 if with the function
having a minimum value at k.
The parabola a >0 a>0 if with the function having a
maximum value at k .
The Vertex Formula
The vertex of the graph of
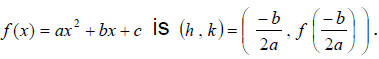
Problem Type #2 :Consider the following quadratic
function
Reduce all fractions to the lowest terms. :
1) Find the vertex of this function.
2) Enter the x- intercept (s), if any, of this function as ordered pair(s).
3) Graph this quadratic function by identifying two points on the parabola other
that the vertex and the x-intercept(s).
EX4:
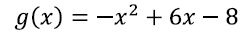
EX5:
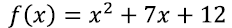
EX6:
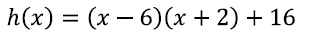
4.2b MAX/MIN APPLICATIONS OF QUADRATIC FUNCTIONS
Problem Type #1:
EX1:
A small cruising ship that can hold up to 56 people provides three-day
excursions to groups of 36 or more . If the group contains 36 people, each person
pays $62. The cost per person is reduced by $1 for each person in excess of 36.
Find the size of the group that maximizes income for the owners of the ship.
Problem Type #2:
EX2:
A rancher has 400 feet of fencing to put around a rectangular field and then
subdivide the field into 3 identical smaller rectangular plots by placing two
fences parallel to one of the field’s shorter sides. Find the dimensions that
maximize the enclosed area.
