Certain functions have inverses. The inverse of a function
will "undo" the action of the original
function. The graphs of a function and its inverse have a beautiful symmetry
across the line
y = x . The symmetry extends to the tangents to the curves. They are all heading
your way in
vivid color!
1. What is an inverse function?
Suppose f :A → B is a function. We know that f is a rule
that maps each element of A to a
unique element of B. Now if there is an inverse function f-1, it will have to
map each
element in the range of f to a unique element in A so that
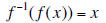for each x in A.
(Also we can see that f must be an inverse function for f-1). We say that f and f-1 are an
inverse function pair.
1.1 Show that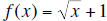 
and g(x)
= (x − 1)^2 are inverse functions, that is, for each x
in [0,∞), g(f (x)) = x and for each x in [1,∞), f(g(x)) = x .
2. What functions have inverses?
Notice the problem if f maps two different x -values, say
x1 and x2 , to the same y in B.
Then how can we construct an inverse function f-1 for f ? We wouldn't know
which x-value
to pick to map back to. We can't choose them both because then f-1would not be
a
function!
We get around this problem by selecting only those
functions that are one-to-one:
A function f :A→B is one-to-one if whenever x1 ≠ x2 in A,
then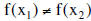 
in B.
2.1 Recall that the horizontal line test is a quick way to
check a graph of a function to
see if the function is 1-1. Just mentally check to see that every possible
horizontal
line can intersect the graph of the function in exactly one place. Check the
graphs
that follow to see whether or not they are one-to-one. Label them and justify
your
answer.
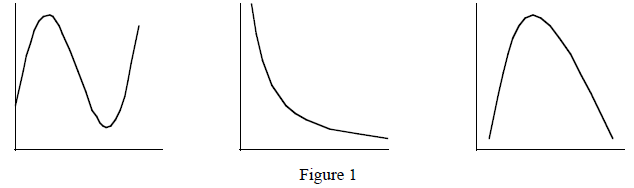
Note that some functions can be made one-to-one by
restricting their domains. For instance
f (x) = x^2 is not one-to-one on (−∞, ∞) but it is on [0, ∞).
3. Symmetry of inverse functions across the line y = x
Symmetry of inverse functions across the line y = x
3.1 Open the Inverse Function tool in the Derivative Kit. Pick any one of the
first
three pairs of inverse functions. Roll the cursor over the graphing plane.
Notice how
corresponding points are reflected across the line y = x . That is, if (a,b) is
on one
curve then (b,a) is on the inverse curve. Explain why this is so in terms of
what
inverse functions do!
3.2 For each function graphed in Figure 2, sketch its
inverse function by reflecting the
curve across the line y = x .
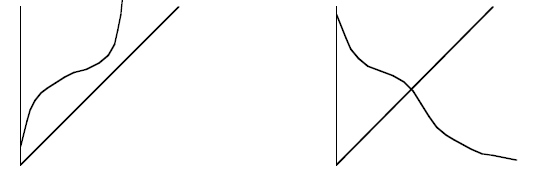
3.3 Now click on the selection box for Tangents. Note that
tangents to the two curves
have the same property of reflecting across the line y = x . State the functions
you
selected (specify constants a and b if appropriate). Sketch the curves and their
tangents on the axes provided.
3.4. In the following true/false questions, use your
knowledge about the domain and range of
a function and your observation of the tool to answer the questions.
a. True or False: If f is continuous and increasing on an interval, then so is f-1on the
corresponding interval.
b. True or False: Dom f-1=Rng f
c. True or False: Rng f-1= Dom f
3.5 Select the third function from the function menu. Note
that g(x) = (x − a)^2 is not
one-to-one over its entire domain (−∞, ∞). Yet it is one-to-one for the Inverses
tool. What is the largest domain over which it is one-to-one (so that the domain
includes the domain shown on the tool)?
3.6 What function on the Inverses tool is it own inverse
for every value of a ? Explain.
3.7 Select the function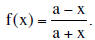 
Using the tool, find the value of a for which the
function is its own inverse and prove that this is the case by direct
substitution .
4. The derivatives of inverse functions
We are going to illustrate the following theorem using the Inverses tool:
Theorem for the Derivatives of Inverse Functions
If a differentiable function f has an inverse function g =
f-1and f′(g(c)) ≠ 0, then gis
differentiable at c and
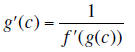
One way of interpreting this statement is to say that
derivatives of the function and its inverse at
corresponding points on their graphs are reciprocals of each other .
This process is easier to see on the Inverses tool than it
is to describe. Click on the Secants
selection box and clear the Tangents selection box to reduce the number of lines
on the screen.
Recall that to find f′(x) we take the limit of the slope
of the secant line from
(x + h, f (x + h)) to (x, f (x)) as h → 0. Notice that as we do this, the rise
over the run for the
corresponding points in the inverse curve are reciprocals relative to the
original curve. Since the
ratios of rise over run are reciprocals at every corresponding point, the
derivatives must also be
reciprocals.
4.1 Let f (x) =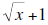 
so
that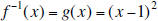 
. So the point (4,3) is on the graph of
f and the corresponding point for g is (3, 4). Use the theorem to calculate
g ′(3) .
5. Important inverse functions: exponential and
logarithmic functions
An important inverse function pair is:
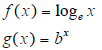for b > 0 and b ≠ 1.
Note that for b = e , we have the natural log and
exponential functions:
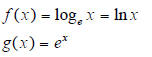
5.1 Move b on the slider as close as possible to e =
2.718...., the base for the natural
logarithms. Label the scale on the axes provided. Sketch the graph of the
inverse
function pair.
