INTRODUCTION TO MATLAB
Chapter 14
Fitting Functions to Data
A common problem that physicists often encounter is to find the best t of a
function (with
a few variable parameters ) to a set of data points. If you are fitting to a
polynomial, then
the easiest way to do this is with polyfit. But if you want to t to a sine, a
cosine, an
exponential, a log , etc., then there is no simple command available. Pay
attention to this
section; it is useful.
14.1 fminsearch
Matlab has a very nice multidimensional minimizer routine called fminsearch that
will do
fits to a general function if you give it a half-decent initial guess for the
fitting parameters.
To see how to use fminsearch generally you can use online help, but here we will
just show
you how to use it for function fitting.
Suppose we have a set of data points (xj , yj) (perhaps read in with Matlab's
load
command as discussed in the Fast Fourier Transform section) and a proposed fitting
function
of the form y = f(x, a1, a2, a3,…). For example, we could try to t to an
exponential
function with two adjustable parameters a1 and a2 as is done in the example in leastsq.m
below:

Or you could t to a cubic polynomial in x2 with four adjustable parameters a1,
a2, a3, a4
with this f:
f(x; a1, a2, a3, a4) = a1 + a2x2 + a3x4 + a4x6 (14.2) (14.2)
which is what polyfit does.
In any case, what we want to do is choose the parameters (a1, a2, a3,
…) in
such a
way that the sum of the squares of the differences between the function and the
data is
minimized, or in mathematical notation we want to minimize the quantity

The first thing you need to do is to make a Matlab M- le called leastsq.m which
evaluates
the least- squares sum you are trying to minimize. It needs access to your fitting
function
f(x, a), which is stored in the Matlab M- le funcfit.m. Here are examples of
these two
files.
This function leastsq.m is the one that you give to fminsearch. It allows
fminsearch
to talk to your fitting function funcfit.m by calculating S from the (x, y) data
and the
an's; it looks like this:
| Example 14.1a (leastsq.m)
% Example 14.1a (Physics 330)
function s=leastsq(a,x,y)
%*********************************************************
% leastsq can be passed to fminsearch to do a
% non- linear least squares fit of the function
% funcfit(a,x) to the data set (x,y).
% funcfit.m is built by the user as described here
% a is a vector of variable parameters; x and y
% are the arrays of data points
%*********************************************************
% find s, the sum of the squares of the differences
% between the fitting function and the data
s=sum((y-funcfit(a,x)).^2); |
| Example 14.1b (funcfit.m)
% Example 14.1b (Physics 330)
function f=funcfit(a,x)
%*********************************************************
% this function evaluates the fitting
% function f(x,a1,a2,a3,...) to be fit to
% data. It is called by leastsq.
% a is a vector of variable fitting parameters a1, a2, ...
% that are used in the function and x is a
% vector of x-values
% the function returns a vector f=f(x,a1,a2,...)
%*********************************************************
% sample exponential function with 2 variable
% parameters
f = a(1)*exp(a(2)*x); |
With these two functions built and sitting in your Matlab directory we are ready
to
do the t. Here is a piece of code that allows you to enter an initial guess for
the fitting
parameters, plot the initial guess against the data, then tell fminsearch to do
the least
squares t. The behavior of fminsearch can be controlled by setting options with
Matlab's
optimset command. In the code below this command is used to set the Matlab
variable
TolX, which tells fminsearch to keep refining the parameter search until the
parameters
are determined to a relative accuracy of TolX. Finally, it plots the best t
against the data.
We suggest you give it a name (perhaps datafit.m) and save it for future use.
The data
needs to be sitting in the le data.fil as two columns of (x; y) pairs, like this
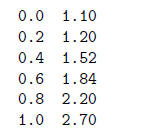
Let's try to t this data to the function f(x) = a1 exp(a2x). Here's the fitting
code
| Example 14.1c (ch14ex1c.m)
% Example 14.1c (Physics 330)
%*********************************************************
% Uses fminsearch to least squares fit
% a function defined in funcfit.m to
% data read in from data.fil
%*********************************************************
clear;close
% read the data file and load x and y
load data.fil;
x=data(:,1);
y=data(:,2);
% set up for the plot of the fitting function
xmin=min(x);
xmax=max(x);
npts=1001;
dx=(xmax-xmin)/(npts-1);
xplot=xmin:dx:xmax;
% set ifit to 0 and don't continue on to the fit until
% the user sets it to 1
ifit=0;
while ifit==0
disp(' Enter an initial guess for the function ')
a=input('parameters [a1,a2,...] in vector form [...]- ')
% plot the data and the initial function guess
yplot=funcfit(a,xplot);
plot(x,y,'b*',xplot,yplot,'r-')
xlabel('x')
ylabel('y')
title('Initial Guess and Data')
ifit=input(' Enter 0 to guess again, 1 to try to fit with this guess - ')
end
%*********************************************************
% Do the fit with the option TolX set; fminsearch will adjust a
% until each of its elements is determined to within TolX.
% If you think fminsearch could do better than it did, reduce TolX.
%*********************************************************
option=optimset('TolX',1e-5);
a=fminsearch(@leastsq,a,option,x,y)
% plot the data and the final function fit
yplot=funcfit(a,xplot);
% Plot the final fit and the data
plot(x,y,'b*',xplot,yplot,'r-')
xlabel('x')
ylabel('y')
title('Final Fit and Data') |
It's a little painful to have to make three les to get this job done, but we
suggest you
learn how to use fminsearch this way. It comes up all the time.
15.1
Matlab's fminsearch can also be used to solve systems of nonlinear equations.
Consider
the following pretty -impossible-looking set of three equations in three unknowns
(x, y, z).
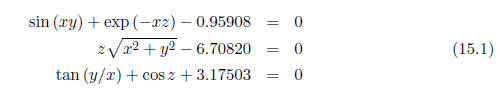
The way to talk fminsearch into solving this set is to invent a scalar function
S(x, y, z)
which consists of the sum of the squares of the three functions given above:
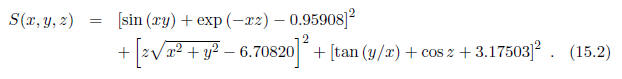
If you look at S(x, y, z) for a bit you will see that (1) it is always positive,
(2) its smallest
possible value is zero, and (3) if you can somehow find values of (x, y, z) that
make it zero,
then you have solved the system of three equations.
Note, however, that fminsearch is a minimizer, not a zero
finder. So it may find a
local
minimum of S(x, y, z) which does not satisfy S = 0. If it fails in this way you
need to (1)
know about it and (2) make another initial guess so fminsearch can take another
crack at
the problem.
Here are two pieces of Matlab code that will use fminsearch to solve systems
like this.
The first one calls fminsearch and the second one, which is a Matlab function
(eqsystem.m)
contains the equations to be solved.
| Example 15.1a (ch15ex1a.m)
% Example 15.1a (Physics 330)
%*********************************************************
% Uses fminsearch to look for solutions to the
% nonlinear system of equations defined in the
% file eqsystem.m
%*********************************************************
clear;
itry=0;
while itry ==0
disp(' Enter an initial guess for the solution')
x=input('of the system of equations in the form [x1,x2,...] - ');
% evaluate the scalar function S(x1,x2,...) so the
% user can see how good the guess is
s=eqsystem(x);
fprintf(' For this guess: S(x1,x2,...) = %g \n',s)
itry=input(' Enter 0 to guess again, 1 to try to solve with this guess- ')
end
x=fminsearch(@eqsystem,x)
s=eqsystem(x);
fprintf(' Final value of S(x1,x2,...) = %g \n',s)
disp(' (Make sure it is close to zero)') |
| Example 15.1b (eqsystem.m)
% Example 15.1b (Physics 330)
function s=eqsystem(xn)
% nonlinear system of equations routine for
% use with zerofinder and fminsearch
x=xn(1);y=xn(2);z=xn(3);
Eq1 = sin(x*y)+exp(-x*z)-0.95908;
Eq2 = z*sqrt(x^2+y^2) -6.70820;
Eq3 = tan(y/x)+cos(z)+3.17503;
s=Eq1^2+Eq2^2+Eq3^2; |
When you solve this system and you are asked for an initial guess, try something
near
(0.8,1.8,2.5).
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
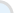 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
April 20th
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
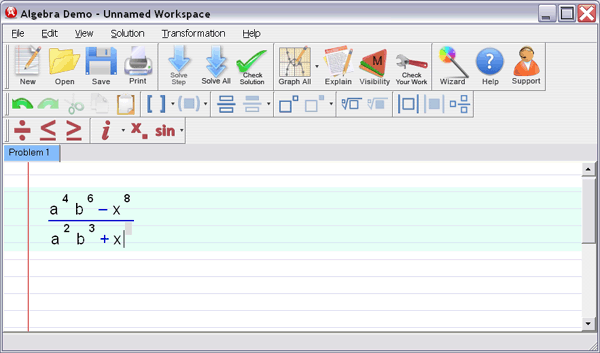
Step 2 :
Let Algebra Helper solve it:
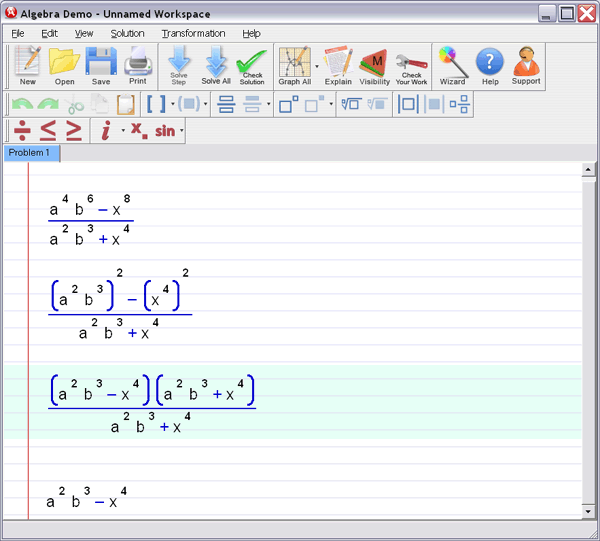
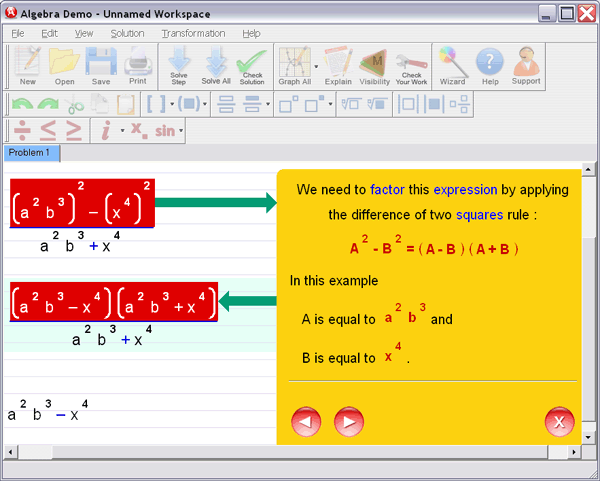
Step 3 : Ask for an explanation for the steps you don't understand:
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



