Definition
A function is a rule that assigns each element in a set A exactly one element in
a Set B.
ยค Each input has only one output!
Example 1
Is the price of a flight a function of the length of the flight?
Solution
This is not a function. The same length of flight can have multiple prices
(where you buy/when you buy/where you sit/how
much baggage).
Example 2
Words
The registrar charges $5 for each transcript. Is this a function?
Hint
input = number of transcripts
output = price
Solution
Yes, there is only one price for any given number of transcripts. That is, each
input has only one output.
Table
Complete the following table.
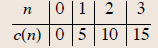where n is the number of transcripts ordered and c (n) is
the cost for n transcripts.
Solution
Graph
Solution
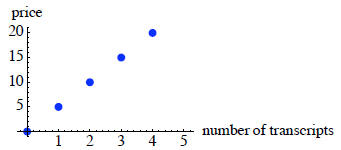
Should we connect the dots?
No! We cannot have partial transcripts.
Graphically, is this a function?
Yes! We can use the vertical line test .
Algebra
(a)
The cost will be equal to 5 times the number of transcripts. c(n) = 5 n
(b)
c (n) represents the cost, in dollars, of buying n transcripts.
c (n) is the dependent variable.
Domain and Range
Domain : the set of whole numbers {0, 1, 2, 3, ...}
Range : 5n where n is a whole number
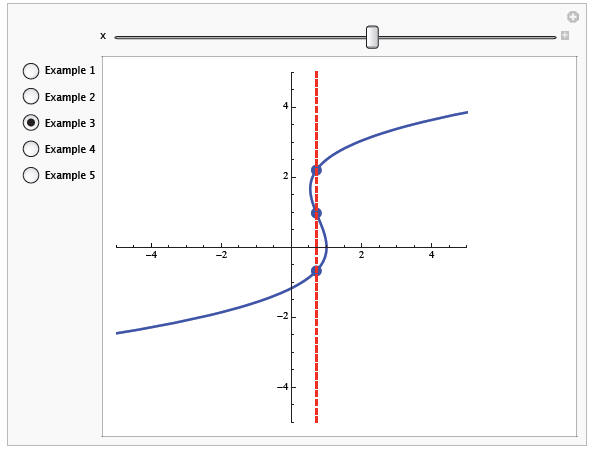
Example 3
(a) Is it a function?
Does each input have only one output? Yes!
(b) Is it a function?
No! -2 goes to 5 and 0.
Example 4
y2 - 4 x3 + 6 = 0
(a) Is y a function of x?
(b) Is x a function of y?
(a) Solve for y . Does every input have only one output?
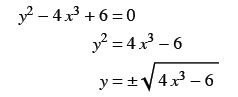
Not a function!
(b) Solve for x. Does every y- value have only one x-value?
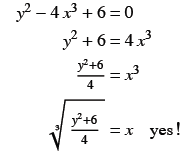
Why are functions helpful?
Prediction and modeling
Vertical Line Test
If we pass a vertical line across the graph and it touches the graph only once
for each vertical line, then each input has only one
output.
Function Notation
Example 1: A quadratic function
Given f (x) = x2 + 3 x, find f (0), f (1), f (x + h),
and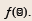 
.
Solution
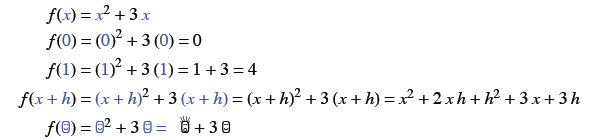
Example 2: A rational function
Given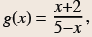 
find g(0), g(5),
g(-2), and g(6).
Solution
More on Function Values
Graphical Manipulate
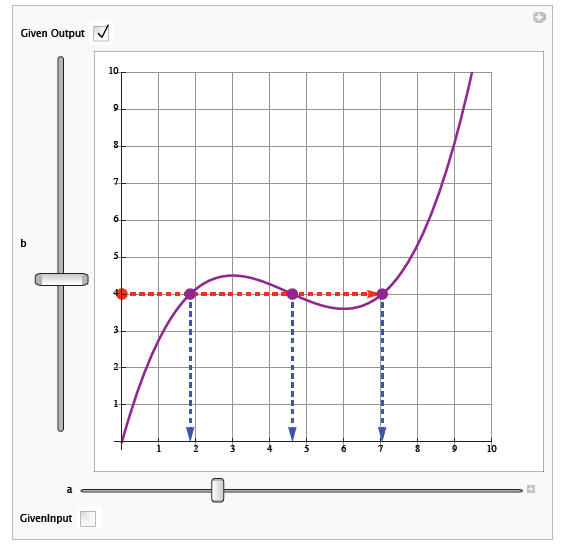
(a) Find f (2).
(b) Find f (7).
(c) Find x such that f (x)
= 7.
(d) Find x such that f (x) = 4 .
Solution
(a) f (2) ≈ 4.2
(b) f (7) ≈ 4
(c) x ≈ 8.6
(d) x ≈ 1.8, 4.6, 7
Graphical Example
Example: Find all x such that f (x) = 0.
f (x) = x(x - 5)2 (2 x + 3)
Solve for x.x(x - 5)2 (2 x + 3) = 0
Solution
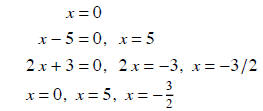
Domain & Range
Terminology
A function assigns each input one and only one output.
Input ---------------------------> Output
The domain of a function is the set of all possible inputs. The range of a
function is the set of all outputs.
Domain -------------------------> Range
The independent variable represents the input of the function. The dependent
variable represents the output of the function.
Independent Variable --------> Dependent Variable
Graphical
Use the graph of f(x) and g(x) below to answer parts a-f. Note that g(x) is the
thicker graph and f(x) is the thinner graph.
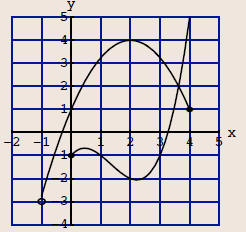
(a) Find the domain of f(x).
(b) Find the range of f(x).
The domain of the thinner function, f (x), is (-1, 4]. This can be written as -1
< x ≤ 4.
The range of f (x) is (-3, 4], that is -3 < y ≤ 4.
Algebraic
Example 1
Find the domain and range of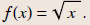 
Solution
We need a nonnegative radicand.
domain : x ≥ 0
range : y ≥ 0
Example 2
Find the domain of
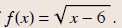
Solution
x - 6 ≥ 0
x ≥ 6
Example 3
Find the domain of
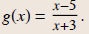
Solution
x ≠ -3
(No division by 0.)
Example 4
Find the domain of
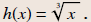
Solution
x ∈R
(all real numbers )
