Equivalent Forms of Algebraic Expressions

Examples

A. Long Division

B. Multiplying by "1"

C. Completing the Square

Practice Problems

Algebra can be used to change the form of many fractional expressions .

Examples:

Basic simplification

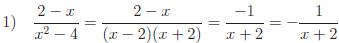
"Rationalizing"
Mult. by 1

Factoring highest power from numerator and denominator

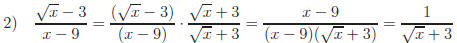
"Do the examples above bring back old (fond?) memories of LIMITS?"

	Separation

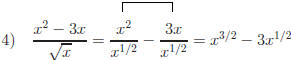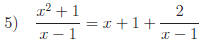Long Division

Mult. by 1

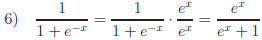
Mult. by 1

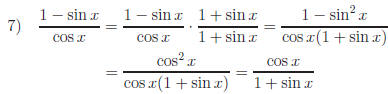
Before we comment on the algebra, let's examine these examples in a cal-
culus context. Since our virtual calculus site is still in development, you'll
need paper and pencil.

Exercise 1: Evaluate the following.

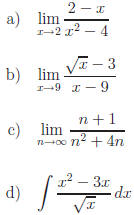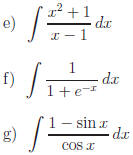Answers	Answers

Note that algebra is essential in evaluating the above limits and integrals.
Another way to evaluate 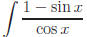would be as follows:

Just for fun (we're not afraid to use fun and calculus in the same sentence),
show both answers to Exercise 1(g) are equivalent .

A. Long Division

A fraction ( rational expression ) that has a monomial denominator, like
Example 4, easily separates. However, if the fraction is improper (degree of
the numerator is greater than or equal to degree of the denominator), then
dividing by a polynomial requires Long Division. Here's Example 5 worked
out.

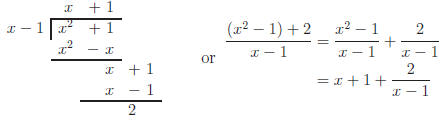
B. Multiplying by "1"

Of our original examples, three of them (#2, 6, and 7) fall into this category.
The integral for sec x is derived using multiplication by a form of 1.

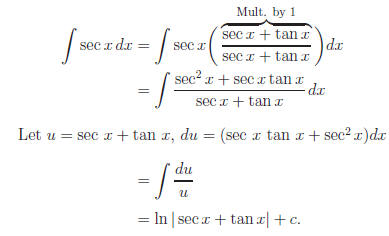
C. Completing the Square

In your previous math courses, completing the square was used to solve
quadratics or to change the form of a second degree polynomial of the type
Ax² + By² + Cx + Dy + E = 0. In Calc II, completing the square will be a
useful (and necessary) tool in evaluating certain integrals.

Illustrations: Complete the square.

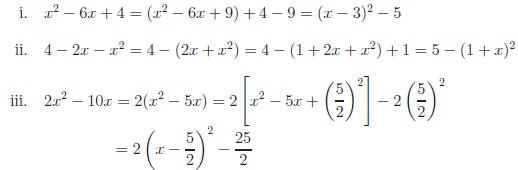
Are you following the process? Maybe you need to try this yourself.

Exercise 2: Rewrite each expression by completing the square.

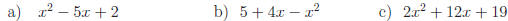
Answers

Now let's try to complete the square starting with the quadratic form
y = ax² + bx + c.

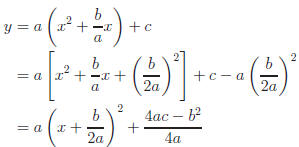
We have completed the square, but what good is this expression? Set y = 0
and find x- intercepts :

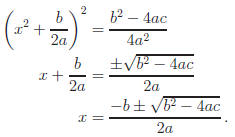
Now you know why math instructors have such a high regard for completing
the square.

We will finish this section with examples of two integrals .

Example.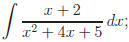

let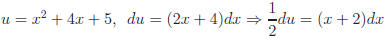

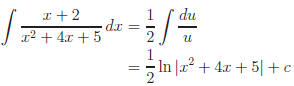
Example.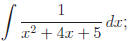

Unlike our first example, substitution won 't work. Let's complete the square
and see what follows.

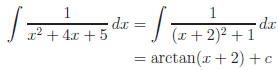
Recall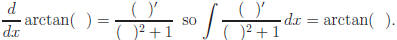 

Conclusion: This review topic (as well as Topics 3 and 4) demonstrates
how algebra is used to evaluate limits and integrals. The challenge is not
just knowing the algebra, but being able to recognize when to apply it. That
only comes from practice.

Practice Problems.

2.1 Find the quotient and remainder:

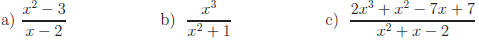
Answers

2.2 All of the following problems require multiplication by a form of 1

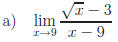Answers
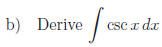Answers
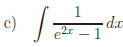Answers
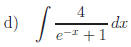Answers

2.3 Complete each square.

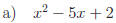Answers

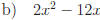Answers

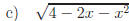Answers

Answers to Practice Problems.

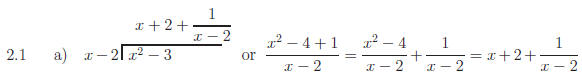
Return to Problem

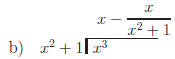
Return to Problem

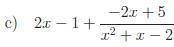
Return to Problem

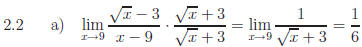
Return to Problem

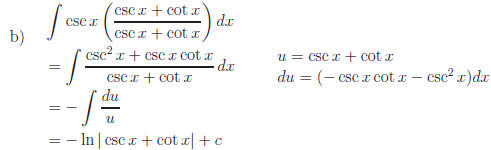
Return to Problem

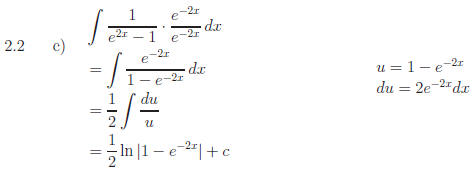
Return to Problem

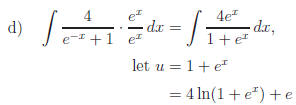
Return to Problem

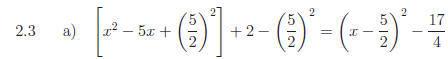
Return to Problem

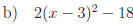
Return to Problem

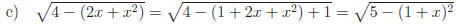
Beginning of Topic

250 Review Topics

250 Skills Assessment

Answers

Recall that for r > 0, as n→∞ OR "When denominator grows fraction approaches 0"

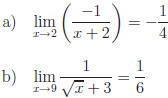
Alternate Method :

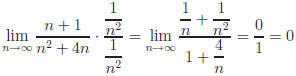
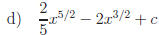
Return to Review Topic

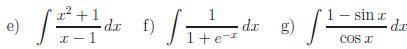
Answers:

e)

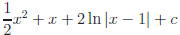
f) Let u = e^x + 1. Why is
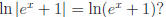
Ans:

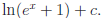
g) Let u = 1+sinx.
Ans:

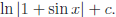
Return to Review Topic

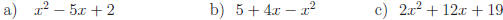
Answers:

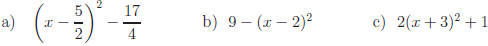
Return to Review Topic