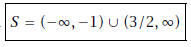Instructions: (100 points) Solve each problem and
box in your final answer.
1. Short responses (10 pts). For True/False responses, you
can use ‘T’ or ‘F’ to represent your answer.
(a) If the coefficient of the x 2 term of a quadratic function is negative, then
the quadratic function
has a…
maximum
minimum
not enough information is
given
(b) If the discriminant of a quadratic equation is
negative, then we can say that…
there are two real solutions
there is only one real
solution
there are no real solutions,
but there are two complex
solutions
(c) F (True/False) A polynomial of degree n has at most n
turning points.
(d) T (True/False) A polynomial of degree n has at most n x-intercepts.
(e) F (True/False) If the degree of the numerator of a rational function is
greater than the
degree of the denominator, then the function has a horizontal asymptote.
§3.1 Complex Numbers (13 points)
2. Calculate each of the following.
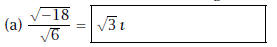
Solution:
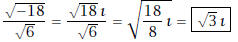
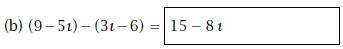
Solution: We have
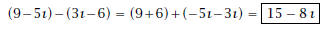
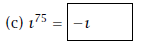
Solution: Compute ı75. We divide 4 into 75
to get a remainder of 3. Thus,
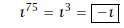
Solution:
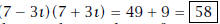
Observe this is the product of conjugate
pairs, and that (a−bı)(a+bı) = a2+b2
3. Calculate
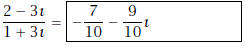
Solution: For division, we first calculate the conjugate
of the denominator, this is 1-3ı. We follow
standard workflow:
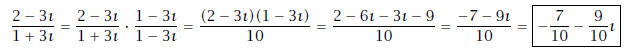
§3.2 Quadratic Functions and Graphs (14 points)
4. Use the Vertex Formula to find the vertex of P(x) = -x2
- 4x + 2. Box in your final answer.
Solution: Indeed,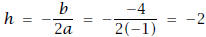
and k = P(h) = P(-2) = -4 + 8 + 2 = 6. The
coordinates of the vertex are V(-2, 6)
5. The following questions apply to the polynomial P (x) =
x2 - 6x + 5.
(a) (5 pts) Complete the square of P.
Answer:
Solution: We follow the algorithm as described in class:
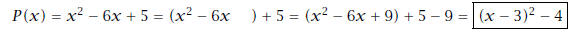
(b) (3 pts) The coordinates of the vertex are V(3,-4)
§3.3 Quadratic Equations (18 points)
6. Solve each of these elementary quadratic equations.
Leave your answer in the boxed region to the
right in the form of a solution set , for example, { 17, 88 } .
(a) (3 pts) x2 = -8
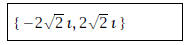
Solution:
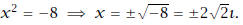
Thus,
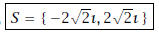
(b) (5 pts) (4x + 1)2 = 20
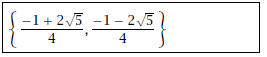
Solution: We have,
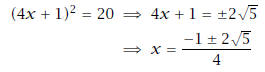
7. Solve each of the following quadratic equations using
the quadratic formula. Leave your answer
as a boxed-in comma-delimited list, for example
7. Solve each of the following quadratic equations using
the quadratic formula. Leave your answer
as a boxed-in comma-delimited list, for example x = 17, 88 .
(a) 2x2 + 3x - 2 = 0.
Solution: We use the Quadratic Formula:
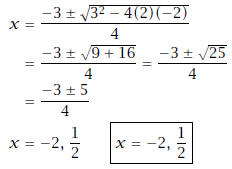
(b) x2 + x + 1 = 0.
Solution: We use the Quadratic Formula:
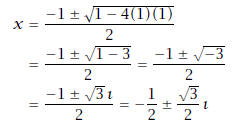
The solutions:
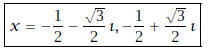
§3.4 Applications (8 points)
8. Find the maximum product of two numbers that sum to 88
by answering each of the following.
For uniformity of notation, let x denote one of the two numbers.
(a) (2 pts) The other number is 88 - x
(b) (2 pts) The product function is P(x) = x(88 - x) = 88x
- x2
(c) (4 pts) Maximum product is Pmax = 1936
Solution: We simply find the coordinates of the vertex
using the infamous Vertex Formula:
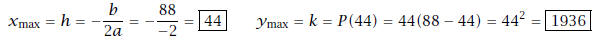
§4.1 Rational Functions and Graphs (10 points)
9. Graph each of the following . Indicate horizontal and
vertical asymptotes using dotted lines , label
their intersection with an axis. Label the x- and y-intercepts, if any.
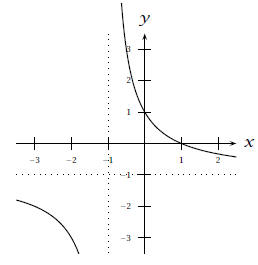
(a) Graph f(x) = 2/(x + 1) - 1
Solution: H.A. y = -1, V.A. x = -1, xintercept
is x = 1, and y-intercept is y = 1.
(b) Graph f(x) = 1/(x - 2)2 + 1
Solution: H.A. y = 1, V.A. x = 2, there
are no x-intercepts, and the y-intercept is
y = 1(1/4) = 5/4.
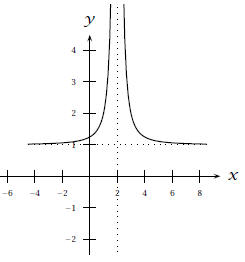
§4.2 More on Graphs of Rational Functions (17 points)
10. List the horizontal asymptotes (H.A.) and vertical
asymptotes (V.A.) of the rational function:
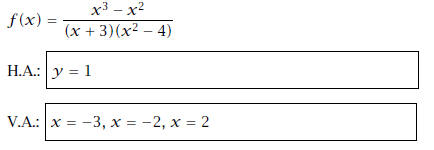
11. Graph the function
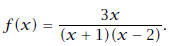Include
all asymptotes and x-intercepts in your graph.
Solution:
H.A. y = 0, V.A. x = -1, x = 2, the x-intercept
is x = 0, and the y-intercept is y = 0. The graph
passes through the origin.
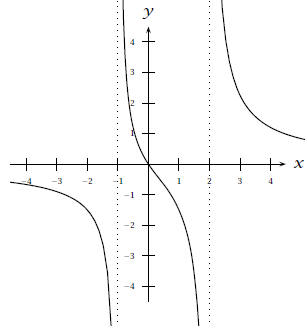
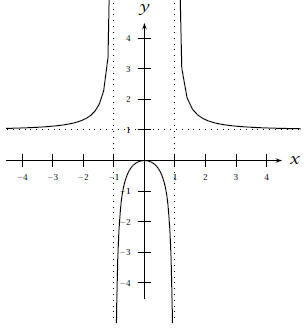
12. Graph the function
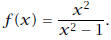Include
all asymptotes and x-intercepts in your graph.
Solution:
H.A. y = 1, V.A. x = -1, x = 1, the x-intercept
is x = 0, and the y-intercept is y = 0. The graph
passes through the origin.
§4.3 Rational Equations and Inequalities (10 points)
13. Solve the equation
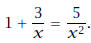Leave your answer as a comma-delimited list of solutions, don’t
forget to box it in.
Solution: Note that there is a natural restriction on the
solution, namely, x = 0. We begin by
multiplying both sides by x2:
 |
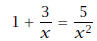given |
 |
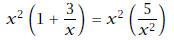multiply both sides by x2 |
| x2 + 3x = 5 |
simplify |
| x2 + 3x - 5 = 0 |
take 5 to LHS |
 |
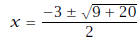apply the quadratic formula |
 |
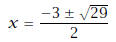Solution: |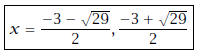
14. Solve the rational inequality: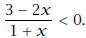
Leave your answer in the form of a solution set. Represent
this solution set using interval notation. Don’t forget to box it in your final
answer.
Solution: Let
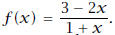This rational function has an x-intercept of x = 3/2 and a vertical
asymptote at x = -1. These points are where the rational expression can change
signs . By taking
some test points we can see that
| Interval |
sign of f |
| x < -1 |
f(x) < 0 |
| -1 < x < 3/2 |
f(x) > 0 |
| x > 3/2 |
f(x) < 0 |
The solution set is then
