Welcome to the third College Algebra test! Your weapons of choice are a pen
or pencil,
this test, and your brains. You are not allowed to use any books, notes (except
the provided
crib sheet), or calculators . Some general hints to help you maximize your
points:
1. Show as much work as you can, since doing so gives me more opportunities
to award
you with partial credit.
2. Don’t spend time converting your solutions to decimal notation — it’s
perfectly acceptable
(in fact, it’ s preferred !) to write 1/3 instead of 0.333 . . . or ln(2) instead
of
0.693 . . ..
3. By the same token, don’t spend too much time expanding polynomials . As a
rule of
thumb, it’s perfectly acceptable to leave any polynomial with a degree higher
than two
in factored form .
4. Be sure to read each question carefully! Failure to do so will result in a
significant loss
of points, even if the answer you arrive at is correct.
5. If you have any questions during the test, don’t hesitate to ask me! If a
problem is
unclear to you, it is probably unclear to your classmates as well.
Good luck, and may the Force be with you!
True & False
1. Mark the following statements as either true or false. If the statement is
false, provide
a counter-example or justification.
(a) (2 points) Every polynomial of degree n has n factors (not all of which
may be
distinct) over the complex numbers
(b) (2 points) If the complex number a +
is a factor of the polynomial p(x), then so
is a −
.
(c) (2 points) Every one-to-one function has an inverse.
(d) (2 points) Every exponential function of the form f(x) = ax, with a > 0,
is a
strictly increasing function.
(e) (2 points) If ax = ay, then x = y.
(f) (2 points) The inverse of a logarithmic function is an exponential
function.
Algebraic Manipulation
2. Solve each equation for x. Be sure to simplify your answer as far as
possible, and convert
any logarithms in your final results to the natural logarithm (“ln”) if
applicable.
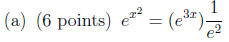
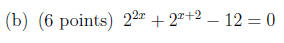
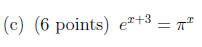
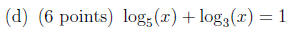
Short Answer
3. (8 points) Factor the polynomial
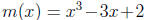using long division and the Rational
Zeros Theorem . (Hint: The Rational Zeros Theorem states that a polynomial of the
form
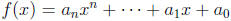can only have rational zeros of the form p/q, where p
is a factor of a0 and q is a factor of an.)
4. (8 points) Write a fifth degree polynomial with real
coefficients that has the roots r 1 = 0,
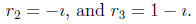
5. (8 points) Let
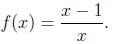
What is f1(x)?
Analysis
6. Consider the exponential function f(x) = 22-x+
1.
(a) (4 points) Draw a graph of f (x) in the space provided.
(b) (6 points) What is the domain of f(x)?
(c) (6 points) What is the range of f(x)?
(d) (4 points) What is f(0)?
(e) (4 points) For what value(s) of x does f(x) = 2?
Applications
7. Consider the case of continuously compounding interest .
(a) (8 points) For fixed principle P, interest rate r, and compounding period n,
how
long will it take double your investment? (Hint: Your annuity is 2P in this
case.
Solve for t.)
(b) (8 points) For fixed principle P, compounding period
n, and time t, what interest
rate is required to double your investment? (Hint: Your annuity is again 2P, but
this time you must solve for r.)
See You Space Cowboys. . .
