I. Betweenness Exercise 3
A) Part 1
1) We are given that A*B*C (Hyp.)
2) We know that for line segment AB to be a part of line
segment AC, any point x on segment
AB must also exist on segment AC; the statements A*x*B and A*B*C must hold true
(Proposition 3.3).
3) Given A*B*C, the line segments AB, AC, and BC can be
represented as the following sets
(suggested by Prof. Smith):
a) Line segment AB is the set of points AB = {x on line AB: A*x*B or x=A or x=B}
(Def. line segment ).
b) The line segment AC is the set of points AC = {x on line AC: A*x*C or x=A or
x=C}
(Def. line segment ).
c) The line segment BC is the set of points BC = {x on line BC: B*x*C or x=B or
x=C}
(Def. line segment).
4) Three cases exist for the placement of x on AB and its
according relationship to AC ( Step 2):
a) Case 1. If x=A, then x lies on segment AC ( Step 3-b).
b) Case 2. If x=B, then x lies on segment AC because we are given that A*B*C
( Steps
1, 3-b).
c) Case 3. If A*x*B, then x lies on segment AC because we are given that A*B*C
and
have specified that x lies on segment AB ( Steps 1, 2, 3-b).
5) Therefore, because any point x on line segment AB is
included in the set of points composing
line segment AC, AB AC (Conc.)
Q.E.D.
A) Part 2
Accordingly, because Betweenness Axiom 1 guarantees
symmetry and distinction given
A*B*C, the set of points on line segment CB is included in the set of points on
line segment CA.
If the “second” of A, B, C is between the “first” and the “third,” then the
“second” is accordingly
between the “third” and the “first” (suggested by Prof. Smith).
B)
1) If A*B*C, then AC AB U BC (Hyp.)
2) The statement that AB U BC implies that any point x is
included in the set of points in line
segment AB or in line segment BC.
3) Consider the addition of the point x to the line that
includes the distinct, collinear points A, B,
and C, provided that x ≠ A, B, or C and x lies on line segment AC (suggested by
Prof. Smith);
additionally , let a distinct line l pass through x.
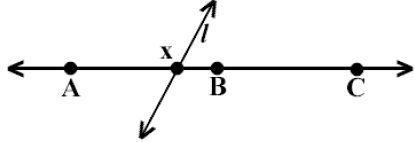
a) If B and C are on the opposite side of A from l, then A*x*B (BA-4), and by
the law of
the excluded middle, x lies on AC (Proof I.A, 4-c).
b) If A and B are on the opposite side of C from l, then B*x*C (BA-4), and x
accordingly lies on AC (Proof I.A, 3-c).
4) Therefore, we know that for any point x lying on AC but
not equal to A, B, or C, either
A*x*B or B*x*C, which accordingly implies that A*x*C. AC AB U BC (Conc.)
Q.E.D.
C)
1) If A*B*C, then AC = AB U BC and B is the only point
common to segments AB and BC
(Hyp., Prop. 3.5.)
2) For this statement to be true, the following statements
must both be valid:
a) AC AB U BC holds (Proof I.B).
b) AB U BC AC holds (Proof I.A).
3) Moreover, B must be the only point common to segments
AB and BC (Step 1).
4) Suppose that a fourth point P is included in AB
 BC such that B*P*C, but P ≠ B (Suggested
BC such that B*P*C, but P ≠ B (Suggested
by Prof. Smith).

5) It is not the case that A*P*B, and it is not the case
that P is equal to A or B ( Step 4).
6) P lies on line segment BC but not on line segment AB
( Steps 4, 5).
7) Therefore, only B intersects with the set of points
included in both line segments AB and BC
(Conc.)
Q.E.D.
II. Betweenness Exercise 16
1) Consider “between” to refer to the midpoint of a line
segment; if A*B*C, then B is the
midpoint of segment AC (AB is congruent to BC).
2) Consider an interpretation in which three distinct,
collinear points A, B, and C exist such that
line segments AB, BC, and AC exist, and such that AB C AC and BC C AC.
3) Segment AB > segment BC.
4) Because segment AB ≠ segments BC, where both segments
are constituents of segment AC,
point B is not the midpoint of AC.
5) By the specified definition of betweenness in this
interpretation, then, it is not the case that
A*B*C.
Q.E.D.
III. Betweenness Exercise 17
1) In order to illustrate the failure of the line separation property in an
interpretation, consider a
model including the distinct, collinear points A, P, B, and D, in which the
Euclidean betweenness
relationships A*P*B, A*B*D, and P*B*D hold.
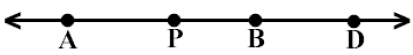
2) Interpret the betweenness of points A, P, and B such
that P*A*B.
3) To show the failure of the line separation property ,
the point P must not lie on either of the
rays formed from the relationship A*B*D (ray BA or ray BD) (Step 1; suggested by
Prof.
Smith).
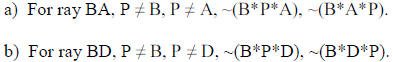
4) Because the point P does not lie on either ray BA or
ray BD, which exist inherently because
the relationship A*B*D has been given (Step 1; Def. opp. rays), the Line
Separation Property
(Prop. 3.4) fails.
Q.E.D.



