1. Use long division to divide f(x) = x4-3x3+x-1 by g(x)
= x2-x+1.
2. Use synthetic division to divide f(x) = x4 - 3x2 + x -
1 by x + 2.
3. Use the remainder theorem to find f(2) if
f(x) = x4 - 3x3 + 2x2 - 6x + 1:
4. Use the factor theorem to determine whether x - 1 is a factor of
f(x) = x5 - 3x3 + x + 1.
5. Find the quotient and the remainder of f(x) = x4 - 3x
+ 1 divided
by x - 3.
6. Use synthetic division , and the fact that -3 is a root
of f (x) =
x3 + 4x2 + x - 6 to express f(x) as a product of 3 linear factors.
7. List all the possible rational zeros of f(x) = 6x3 -
5x2 + 4x - 15
determined by the Rational Zero Theorem .
8. Use the Upper and Lower Bound Theorem to determine upper and
lower bounds for the roots of f (x) = 4x3 - 3x2 + 5x - 7.
9. Use Descartes’ Rule of Signs to determine the possible
numbers of
positive and negative roots of f(x) = x5 - 4x3 + 3x + 1.
10. Use the general strategy developed in section 3.3 to
find all the real
zeros of g (x) = 2x4 + x3 - 11x2 - 4x + 12.
11. Show that all the roots of h(x) = 10x3+51x2+98x+177
lie between
x = -6 and x = 1.
12. Show that f(x) = x3 + 3x - 5 has a zero between x = 1
and x = 2.
Estimate this zero to within 1/4.
13. Determine the multiplicities of the zeros of f(x) =
x3(x-1)5(x+3)2.
Then graph the function .
14. Find a polynomial f of degree 2 which has 1+i as a
zero and which
satisfies f(2) =-1.
15. Use the zero -1 + 2i of f(x) = x4 + 2x3 + 6x2 + 2x + 5 to find all
the zeros.
16. Use the graph of f (x) =1/x to graph
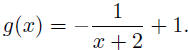
17. Find the horizontal asymptote of the function
.
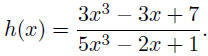
18. Find the vertical asymptotes of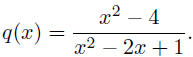 
19. Determine whether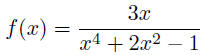 
is even or odd.
20. Use the general strategy to graph the rational function
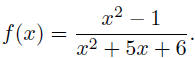
21. Suppose that a company has fixed costs of $2000 per
month and
each unit that it produces costs $10 to make. Find a formula for the cost
function C(x) to produce x units. Then find a formula for the average cost
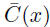per unit, and explain the meaning of the
horizontal asymptote of the
function.
