Unit 6: Polynomials and The Role of the Distributive Property
A quadratic expression is just a special case of a polynomial expression. A
polynomial is then defined, and examples are used to illustrate the connections
between quadratics and polynomials . Important vocabulary for polynomials is
defined, including degree and leading coefficient. Operations on polynomials
are mastered, including addition, subtraction, and multiplication.
Multiplication of polynomials is not strictly held to binomials and the FOIL
method, rather the
concept of distribution is used to show that polynomials of more than two terms
can also be multiplied.
The focus of the unit then shifts to a discussion of factoring. As an
introduction to factoring, the case of the difference of squares is discussed in
terms of
the solution to the equation
.
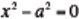Namely, that the since the solutions to that equation, a and –a, are just the
roots of the function, the equation can
be written as (x + a)(x - a) = 0. Factoring out the GCF is then reviewed from
the first unit and expanded to include more complex polynomials. This
concept is expanded to develop the method of factoring by grouping. For example,
the expression x3 + x2 + 2x + 2 is written as
x2(x +1) + 2(x +1) and
then the
(x +1) term is factored out so that the final factorization is
(x2 + 2)(x +1).
This method is then applied to factor quadratic expressions of the form
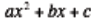by first
multiplying
a- c and then determining the pair of factors of
ac whose sum is b. Then, b is rewritten using this pair of factors, and the
method of factoring by grouping is used. For example, the expression
2x2 + 5x + 2 is written as
2x2 + 4x + x + 2, and then factored into
(2x +1)(x + 2). Factoring quadratics of the form
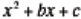is introduced only as a
special case of the standard form of a quadratic.
The use of the zero product property is employed throughout the section on
factoring in order to solve factorable quadratic equations. An emphasis is
placed on the distinction between factoring an expression and solving an
equation. Finally, division of polynomials is explored and the role of factoring
in
reducing such an expression to lowest terms is discussed.
| # |
Learning Targets |
Stand
ard |
Textbook |
Active Practice |
| 6A |
Define polynomial, identify the
degree of polynomials, and provide examples of
expressions that are polynomials. |
10.0 |
|
|
| 6B |
Add and subtract polynomials and
explain how the two operations on polynomials are
related. |
10.0 |
|
|
| 6C |
Multiply two or more binomials and
explain the role of the distributive property |
10.0 |
|
|
| 6D |
Multiply many polynomials and explain
how the distributive property is related to
polynomial multiplication. |
10.0 |
|
|
| 6E |
Explain the relationship between the
multiplication of polynomials and factoring
polynomials. |
10.0, 11.0 |
|
|
| 6F |
Factor a difference of two squares
polynomial . |
11.0 |
|
|
| 6G |
Factor out the GCF from polynomials
with many terms. |
11.0 |
|
|
| 6H |
Factor a polynomial expression by
grouping and identify algebraic properties that are used
in the process. |
11.0 |
|
|
| 6I |
Use factor by grouping to factor
quadratic expressions that are in standard form (ax2+bx
+c). |
11.0 |
|
|
| 6J |
Solve quadratic equations by
factoring and using the Zero Product Property and explain
the process of doing so. |
11.0
14.0 |
|
|
| 6K |
Use factoring to find the roots of a
factorable quadratic equation. |
11.0 |
|
|
| 6L |
Explain the difference between
solving a quadratic equation by factoring and factoring a
quadratic expression. |
11.0, 14.0 |
|
|
| 6M |
Use factoring to simplify expressions
(reducing) involving polynomial division. |
10, 11.0 |
|
|
| 6N |
Explain and provide justification for
my reasoning why polynomials cannot be divided “term
by term.” |
10.0 |
|
|
Essential Standards (CA):
10.0: Students add, subtract, multiply, and divide monomials and polynomials.
Students solve multi-step problems, including word problems, by using these
techniques.
11.0: Students apply basic factoring techniques to second- and simple
third-degree polynomials. These techniques include finding a common factor for
all
terms in a polynomial, recognizing the difference or two squares, and
recognizing perfect squares of binomials.
Supporting Standards: Algebra 1:
12.0: Students simplify fractions with polynomials in the numerator and
denominator by factoring both and reducing them to the lowest terms.
21.0: Students graph quadratic functions and know that their roots are the
x-intercepts.
14.0: Students solve a quadratic equation by factoring or completing the square.
22.0: Students use the quadratic formula or factoring techniques or both to
determine whether the graph of a quadratic function will intersect the x-axis in
zero, one, or two points.
24.0: Students use and know simple aspects of a logical argument.
25.0: Students use properties of the number system to judge the validity of
results, to justify each step of a procedure, and to prove or disprove
statements
Unit 7: Rational Expressions
Rational expressions are built by dividing two polynomial expressions, called
N(x) for numerator and
D(x) for denominator. The concept of writing a
rational expression in lowest terms using factoring N(x) and D(x) is expanded
from the previous unit, and provides a foundation for performing the operations
of multiplication and division on rational expressions. A comparison of
different methods of multiplying rational expressions (i.e. multiply across, or
factor
then simplify) illustrates another need for factoring polynomials. The
operations of multiplication and division on rational expressions are
consistently
compared with the same operations on rational numbers.
Continuing with the four operations, the addition and subtraction of rational
expressions is discussed for like denominators . Emphasis is placed on
distributing the negative sign in the numerator of the second rational
expression when subtracting. The concept of least common denominator (LCD) is
reviewed with rational numbers, and the LCD of multiple
rational expressions is found, and used to rewrite expressions with common
denominators. Addition
and subtraction of rational expressions with unlike denominators is discussed
with increasingly more complex examples, while still bridging connections to
addition and subtraction of rational numbers.
| # |
Learning Targets |
Stand
ard |
Textbook |
Active Practice |
| 7A |
Explain the process of simplifying a
rational expression by factoring and reducing to lowest
terms. |
12.0 |
|
|
| 7B |
Explain why factoring is needed in
multiplication and division, as opposed to just
multiplying “straight across.” |
12.0 |
|
|
| 7C |
Multiply rational expressions and
simplify to lowest terms. |
13.0 |
|
|
| 7D |
Divide rational expressions and can
explain the process of doing so. |
13.0 |
|
|
| 7E |
Explain the relationship between the
multiplication of and division of rational expressions. |
13.0 |
|
|
| 7F |
Add and subtract rational expressions
with like denominators. |
13.0 |
|
|
| 7G |
Find the least common denominator of
two or more rational expressions and explain the
process of how this is done. |
12.0 |
|
|
| 7H |
Use the least common denominator to
write two or more rational expressions with the
same denominator and then add or subtract them. |
12.0, 13.0 |
|
|
| 7I |
Explain how to simplify rational
expressions that involve addition, subtraction,
multiplication, and division |
13.0 |
|
|
Essential Standards (CA):
12.0: Students simplify fractions with polynomials in the numerator and
denominator by factoring both and reducing them to the lowest terms.
13.0: Students add, subtract, multiply, and divide rational expressions and
functions. Students solve both computationally and conceptually challenging
problems by using these techniques.
Supporting Standards:
11.0: Students apply basic factoring techniques to second- and simple
third-degree polynomials. These techniques include finding a common factor for
all
terms in a polynomial, recognizing the difference or two squares, and
recognizing perfect squares of binomials.
15.0: Students apply algebraic techniques to solve rate problems, work problems,
and percent mixture problems.
24.0: Students use and know simple aspects of a logical argument
25.0: Students use properties of the number system to judge the validity of
results, to justify each step of a procedure, and to prove or disprove
statements.
Unit 8: Working with Inequalities
This unit is the capstone of the course, in which many essential concepts are
reviewed and expanded in the context of inequalities. The unit begins with
situational word problems and the writing of inequalities that represent those
particular situations. The graphs of basic inequalities on a number line are
reviewed. This knowledge is then used to solve and graph the solution set of a
linear inequality in one variable. It is emphasized that whenever multiplying
or dividing by a negative number in any inequality, the direction of the
inequality sign changes. Problems are solved using linear inequalities in one
variable.
The concept of absolute value as distance from 0 is revisited. Compound
inequalities are used to solve absolute value inequalities in one variable.
Knowledge of graphing linear equations provides the foundation for graphing
solution sets of inequalities in two variables. The solution set of a linear
inequality in one variable is graphed in the coordinate plane . The graphs of
inequalities in one and two variables are compared (e.g. compare
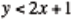
and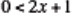 
). A comparison of the behavior of the boundary point and boundary line for
both one and two variable linear inequalities is explored. The
solution sets of systems of linear inequalities are also identified and graphed.
These systems in two variables may have more than inequalities. Continuing
the discussion of inequalities in two variables, quadratic inequalities are
explored, as well as systems mixed with quadratic and linear inequalities.
| # |
Learning Targets |
Stand
ard |
Textbook |
Active Practice |
| 8A |
Use inequalities in one and two
variables to algebraically represent real world situations
and explain reasoning behind the mathematical model . |
5.0 |
|
|
| 8B |
Draw the graph of an inequality based
on a verbal description and justify the diagram |
4.0 |
|
|
| 8C |
Determine the solution set of a
linear inequality in one variable and graph |
4.0 |
|
|
| 8D |
Solve absolute value inequalities in
one variable and explain how they are visually
represented on the number line and why absolute value is necessary to
describe the
situation. |
3.0 |
|
|
| 8E |
Graph the solution set of a linear
inequality and explain the process used to find the
solution |
6.0 |
|
|
| 8F |
Explain the relationship between the
boundary point of a one variable inequality and the
boundary line of a two variable inequality |
6.0 |
|
|
| 8G |
Graph the solution set of a system of
linear inequalities, including systems with two
variables, and two inequalities. |
9.0 |
|
|
| 8H |
Graph the solution set of a quadratic
inequality and justify that the solution set is accurate |
21.0 |
|
|
| 8I |
Graph systems of inequalities
including systems with quadratic inequalities and relate the
concept of the boundary curve of a quadratic inequality, with the
concepts of the boundary
point and boundary line. |
21.0 |
|
|
| 8J |
Solve real world problems that
require mathematical models involving inequalities |
5.0 |
|
|
Essential Standards (CA):
3.0: Students solve equations and inequalities involving absolute values.
4.0: Students simplify expressions prior to solving linear equations and
inequalities in one variable, such as 3(2x – 5) + 4(x – 2) = 12.
6.0: Students graph a linear equation and compute the x- and y-intercepts (e.g.,
graph 2x + 6y = 4). They are also able to sketch the region defined by linear
inequality (e.g., they sketch the region defined by 2x + 6y < 4).
9.0: Students solve a system of two linear equations in two variables
algebraically and are able to interpret the answer graphically. Students are
able to solve
a system of two linear inequalities in two variables and to sketch the solution
sets.
Supporting Standards:
5.0: Students solve multi-step problems, including word problems, involving
linear equations and linear inequalities in one variable and provide
justification
for each step.
15.0: Students apply algebraic techniques to solve rate problems, work problems,
and percent mixture problems.
21.0: Students graph quadratic functions and know that their roots are the
x-intercepts.
24.0: Students use and know simple aspects of a logical argument:
25.0: Students use properties of the number system to
judge the validity of results, to justify each step of a procedure, and to prove
or disprove statements.
Unit 10: CST Review Unit
In this final unit, the connections that have been formed from unit to unit are
solidified. The relationships between all the skill sets and concepts that have
been learned throughout the course are communicated. As a way of differentiating
instruction, understanding of skills and concepts from the course is
self-assessed,
and an individualized plan is developed to address any deficiencies.
