You have already learned how to add or subtract two
fractions with the same
denominators: just add (or subtract) the numerators of the fractions :
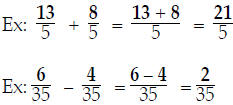
However, to add fractions with different
denominators, it's necessary to convert the
fractions to equivalent ones , which have the same denominator:
In this example, finding the common denominator was
pretty easy. The common
denominator is 6. We found it by multiplying the original denominators, 2
and 3.
Notice that 2 and 3 are both prime numbers.
What happens if the beginning denominators are not prime numbers?
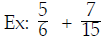
We could find a common denominator as we did before: just
multiply 6 and 15 together:
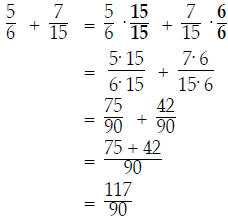
This involved a lot of work! Also, although it may not be
obvious, the final answer is
not in lowest terms ; the fraction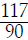
can
be reduced :
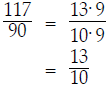
We can save ourselves from working with larger numbers by
finding the Least
Common Denominator (LCD). The process for finding the LCD is outlined below;
but
before we look at it, consider this: The " LCD process " is more complicated than
simply
multiplying denominators together, and seems hard when you first learn it; but
it's
worth the effort. Here are its advantages:
• Systematic . Once you learn this method, it eliminates guess work.
• It allows you to work with smaller numbers.
• Most importantly, the same method has to be used for problems that come up
later
in Algebra.
Now we outline the LCD process. The process is based on factoring. It has
three steps.
To find the LCD ( Least Common Denominator) of two or more fractions:
LCD PROCESS
1. Factor each denominator into prime numbers.
Use exponential notation for the result. If a denominator is already
prime, this
step is easy.
2. List all the different prime numbers that appeared in Step 1.
3. Raise each prime number to the largest exponent it receives in
any of the
factorizations. Then multiply these together. |
Here's an example: we will find the LCD of the following
fractions (we won't bother to
carry out the addition of the fractions in this example).
Ex: Given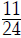 
and
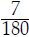. What is the LCD of these two fractions ?
Step 1. Factor 24 and 180, using exponential notation:
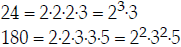
Step 2. List all the different prime numbers in
Step 1:
2, 3, 5 are all the prime numbers that occurred.
(Notice that 2 and 3 occurred in both factorizations , and 5
occurred only in the second factorization.)
Step 3. Raise each prime number to its highest power, and multiply:
The first prime is the number 2. It's raised to the third power in the first
factorization, and it's raised to the second power in the second factorization.
So its
highest power is 3. Write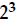 
.
The second prime is 3. It's raised to the first power (so no exponent is
written; 31
= 3) in the first factorization, and it's raised to the second power in the
second
factorization. So its highest power is 2. Write
.
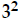The third prime is 5. It's not in the first factorization, and it's raised to
the first
power in the second factorization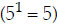 
. So its
highest power is 1, which we don't
need to write. We write only 5.
