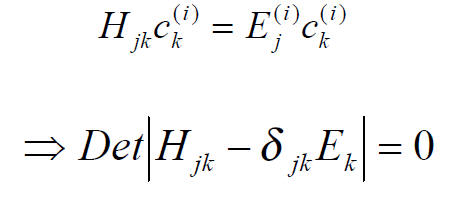TRANSFORMATION TO DIAGONAL MATRICES

a) Linear transformations

Suppose you take every vector (in 3 dim. Space) and multiply it by 17, or you rotate every vector
by 39° about the z-axis, or reflect every vector in the x-y-plane - these are all examples of
LINEAR TRANSFORMATIONS .

A linear transformation (T) takes each vector in a vector space and “transforms” it into some
other vector.

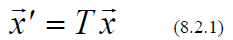
with the provision, that the operation is linear (see Definition linear operator -> our operators are
linear transformations)

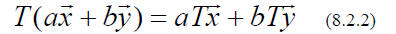
If we know what a particular linear transformation does to a set of BASIS vectors (they span the
vector space), one can easily figure out what it does to ANY vector.

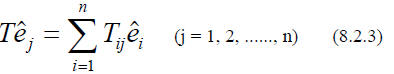
If I choose this form, the vector is in form of a row vector.
If 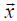is an arbitrary vector :

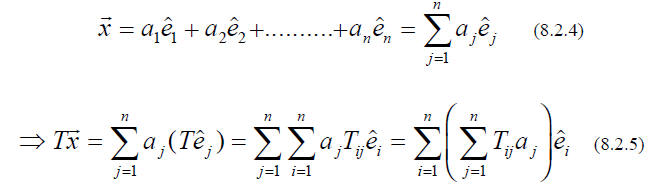
Evidently T takes a vector with components 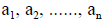into a vectpr with components

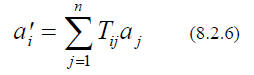
Thus the n² ELEMENTS T_ij uniquely characterize the linear transformation T (with respect to a
given basis ) just as the n components ai uniquely characterize the vector 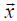(with respect to the
same basis)

If the basis is orthonormal

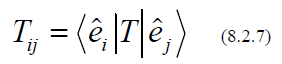
The study of linear transformations reduces then to the theory of matrices.

SUM :

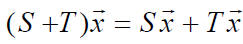
match the rule for adding matrices

PRODUCT : 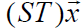Net effect of performing them in succession, first T, then S.

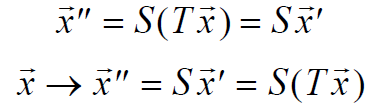
Which matrix A represents the combined transformation ?

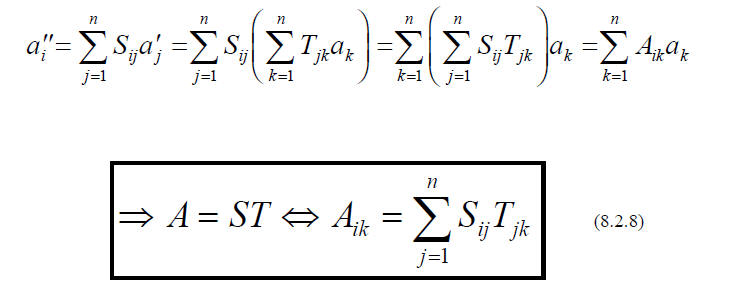
The components of a given vector depend on your (arbitrary) choice of basis vectors, as do the
elements in the matrix representing a linear transformation.
We might inquire how these numbers change , when we switch to a different basis. The new basis
vectors, , are - like ALL vectors - linear combinations of the old ones.

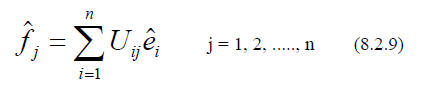
This is ITSELF a linear transformation ( Compare (8.2.3)), and we know immediately how the
components transform:

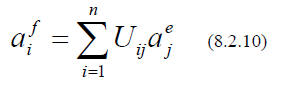
where the superscript indicates the basis.
In matrix form

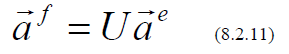
What about the matrix representing a given linear transformation, T ?
In the old basis we had

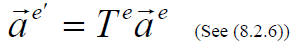
and from (8.2.11) we obtain after multiplying both side by U^-1

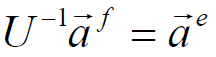
Note that U^-1 certainly exists - if U were singular, then the 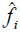would not span the space, so
they would not constitute a basis.

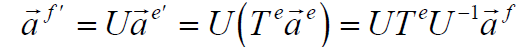
Evidently

In general, two matrices (T₁ and T₂) are said to be SIMILAR, if T₂ = UT₁U^-1 for some (non singular) matrix U.

What we have just found is, that similar matrices represent the same linear transformation
with respect to two different bases .
If the first basis is orthonormal, the second one will also be orthonormal, if and only if the
matrix U is unitary. Since we always work in orthonormal bases, we are interested mainly in
unitary similarity transformations.
While the ELEMENTS of the matrix representing a given linear transformation may look very
different in the new basis, two numbers associated with the matrix are unchanged : the
determinant and the TRACE.
The determinant of a product is the product of the determinants, and hence

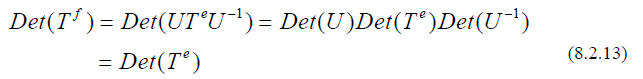
And the TRACE, which is the sum of the diagonal elements

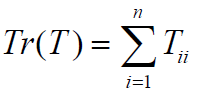
has the property that

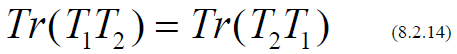
(For any two matrices T₁ and T₂ ), so that

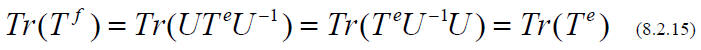
For an orthogonal transformation 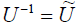If we had assumed vectors with complex
components, with the norm

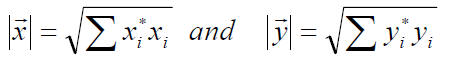
we would have a unitary transformation instead of an orthogonal one.

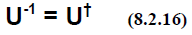
A very important unitary transformation is the one of a Hermitian matrix into a diagonal matrix.

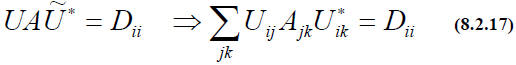
EIGENVECTORS AND EIGENVALUES.

Consider the linear transformation in 3-dim. space consisting of a rotation about some specified
axis by an angle θ. Most vectors will chnage in arather complicated way (they ride around on a
cone about the axis), but vectors that happen to lie ALONG the axis have a very simple
behavior : They don’t change at all 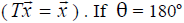then vectors, which lie in the

“equatorial” plane reverse sign, 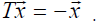. In a complex vector space, EVERY linear
transformation has “special” vectors like these, which are transformed into simple multiples of
themselves:

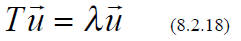
{This is NOT always true in REAL vector space (where the scalars are restricted to real values )}

They are called EIGENVECTORS of the transformation, and the (complex) number , λ , is their
EIGENVALUE.
The NULL vector does not count, even though, in a trivial sense, it obeys (8.2.18) for ANY T
and λ, an eigenvector is any NONZERO vector satisfying (8.2.18)
Notice that any (nonzero) multiple of an eigenvector is still an eigenvector with the same
eigenvalue.
With respect to a particular basis, the eigenvector equation has the matrix form

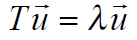(8.2.19) (for nonzero 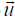or

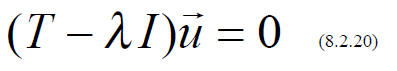
Here 0 is the ZERO MATRIX, whose elements are all zero .

Now, if the matrix (T - λI) had an inverse, we would multiply both sides of (8.2.20) by
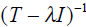and conclude that
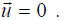
But by assumption 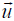is not zero, so the matrix (T - λI) must in fact be singular, which means
that the determinant vanishes.

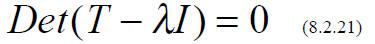
SECULAR or CHARACTERISTIC EQUATION

This yields an algebraic equation for λ of n^th order, where the coefficients depend on the elements
of T. Its solution determines the eigenvalues. n^th order equation -> n (complex)
roots.

(It is here that the case of real vector spaces becomes more awkward, because the
characteristic equation need not have any (real) solutions at all)

However, some of these may be duplicates, so all we can say for certain is, that an n x n matrix
has AT LEAST ONE and MOST n DISTINCT eigenvalues. To construct the corresponding
eigenvectors it is generally easiest simply to plug each λ back into (8.2.19) and solve “by hand”
for the components of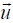
A matrix can be diagonalized, if it is either
1) unitary
2) hermitian
or 3) all eigenvalues are different.

Now, I show an example

Diagonalization of a Matrix

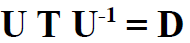
Task to find U and U^-1

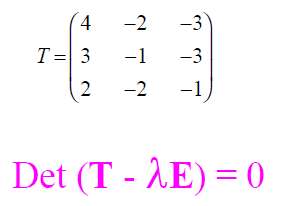
SECULAR or CHARACTERISTIC EQUATION

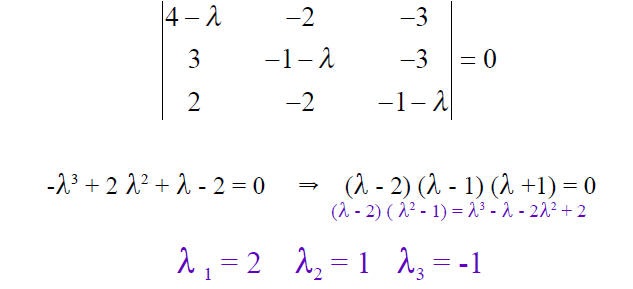
The eigenvectors are:

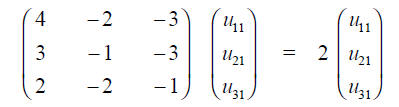
I use here the second index to indicate to which eigenvalue (1,2,3) the eigenvector u
belongs

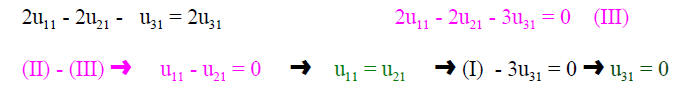
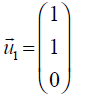
Analog

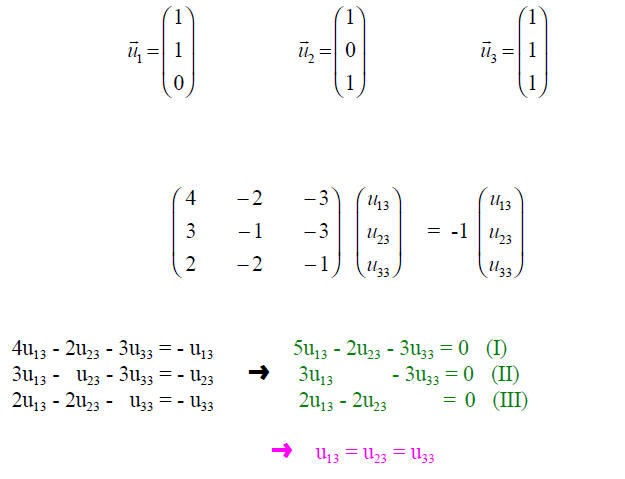
If we ask ourselves which matrix will achieve the diagonalization of T , we find that
the matrix which accomplishes the transformation can be constructed by using the
eigenvectors as the columns.

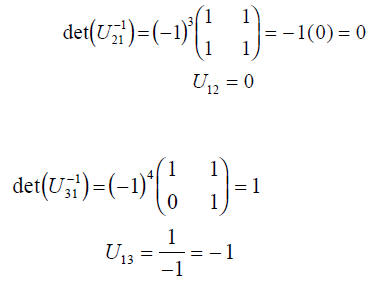
etc

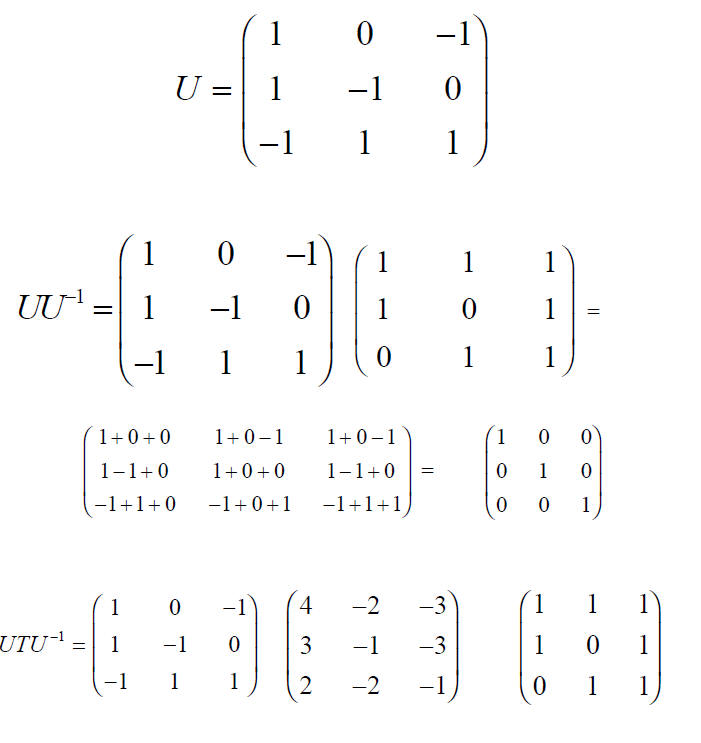
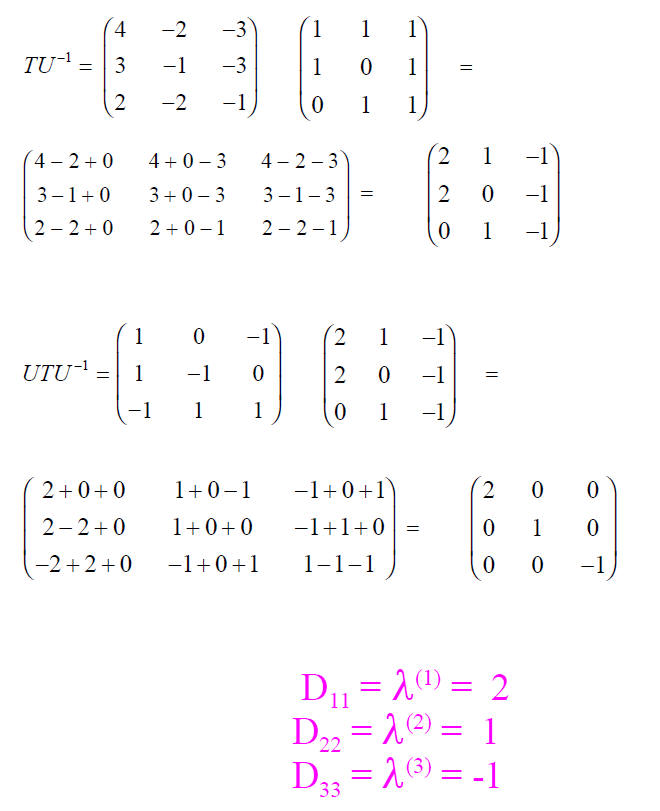
The Schroedinger eigenvalue problem

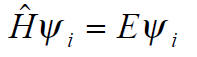
can be converted easily into the matrix eigenvalue form

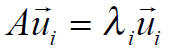
In order to see this, we expand 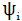using an arbitrary complete orthonormal set

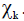
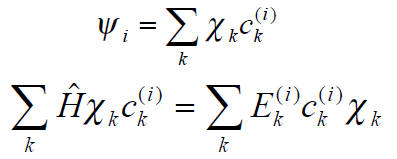
We multiply from the left with 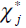and integrate