Theorem 5.5 Log Rule for Integration
Let u be a differentiable function of x.
Because du = u’dx, the second formula can also be written
as
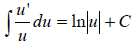
Ex 1 Find the indefinite integral.
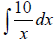
Ex 2 Find the indefinite integral.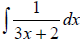
Ex 3 Find the indefinite integral.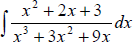
Ex 4 Find the indefinite integral by u- substitution .
(Hint: Let u be the
denominator of the integrand .)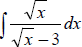 
Ex 5 Find the indefinite integral. You may have to use
long division first .
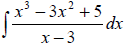
Guidelines for Integration
1. Learn a basic list of integration formulas. (Including those given in
this section you now have 12 formulas: the Power Rule , the Log Rule ,
and ten trigonometric rules . By the end of Section 5.7, this list will
have expanded to 20 basic rules.)
2. Find an integration formula that resembles all or part of the integrand,
and, by trial and error, find a choice of u that will make the integrand
conform to the formula.
3. If you cannot find a u- substitution that works , try altering the
integrand. You might try a trigonometric identity, multiplication and
division by the same quantity, or addition and subtraction of the same
quantity. Be creative.
4. If you have access to computer software that will find antiderivatives
symbolically , use it.
Ex 6 Find the indefinite integral: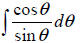
Integrals of the Six Basic Trigonometric Functions
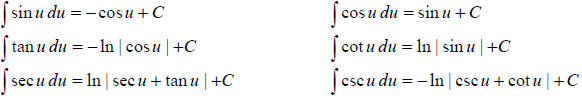
Ex 7 Solve the differential equation. Use a graphing
utility to graph three
solutions , one of which passes through the given point.
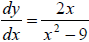,(0,4)
Ex 8Evaluate the definite integral. Use a graphing utility
to verify your
result.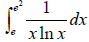
Ex 9 Find the area of the region bounded by the graphs of
the equations .
Use a graphing utility to verify your result.
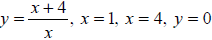
Ex 10 Find the average value of the function over the
given interval.
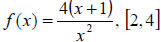
5.2 Homework # 1 – 73 e.o.o. and 85, 87, 91
