Solving quadratic equations

Project 1 will be to implement a finite element method for a two-point boundary- value problem . It will
have several parts.

Warmup: Solving quadratic equations

The quadratic formula says that the solutions of ax ² + bx + c = 0 are given by

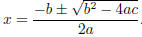
If b² − 4ac < 0 then √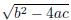 is imaginary, so there is no problem with round-off error.
If b² − 4ac > 0 then cancellation can occur in 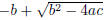if b > 0 and in 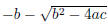if b < 0.
Thus, if b > 0 one would want to use the computations

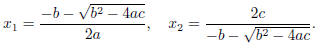
Similarly if b < 0.
Write a function (quadratic- solver a b c ) that returns a list of the two roots of ax² + bx + c = 0 as
accurately as possible. Test your code on the following problems:

euler-126% gsi
Gambit v4.1.2
> (sqrt -1)
+i
> (sqrt +i)
.7071067811865476+.7071067811865475i
> (load "quadratic-solver")
"/export/users/lucier/programs/615project/2007/project-1/quadratic-solver.scm"
> (quadratic-solver 1 2 5)
(-1+2i -1-2i)
> (quadratic-solver 1 -1 1)
(1/2+.8660254037844386i 1/2-.8660254037844386i)
> (quadratic-solver 1 2 -1)
(-2.414213562373095 .4142135623730951)
> (quadratic-solver 4 1 1)
(-1/8+.4841229182759271i -1/8-.4841229182759271i)
> (quadratic-solver 4 4 1)
(-1/2 -1/2)
> (quadratic-solver 4 0 1)
(+1/2i -1/2i)
> (quadratic-solver 0 0 1)

*** ERROR IN (console)@11.1 -- not a quadratic: 0 0 1

1>
> (quadratic-solver 4 0 -1)
(-1/2 1/2)
> (quadratic-solver 1 3138428376721 1)
(-3.138428376721e12 -3.186308177103568e-13)
>

*** EOF again to exit

Meroon

Standard Scheme (so-called R5RS Scheme, which Gambit implements) does not have an object system.
We use an object system provided by the software package Meroon.

To use Gambit, you need to have /pkgs/Gambit-C/current/bin/ in your path. The Gambit interpreter
is called gsi and the Gambit compiler is called gsc.

To have Gambit load Meroon automatically, just call gsi++ or gsc++.

Our system has two differences with standard Meroon:

(1) In standard Meroon, keywords begin with a colon; in our Meroon keywords end with a colon:
(define-class Polynomial Object
((= variable immutable:)
(= terms immutable:)))

(2) In standard Meroon, so-called setters begin with set- and end with !. In our Meroon, setters end
with -set!:

euler-130% gsi++
[ Meroon V3 Paques2001+1 $Revision: 1.1 $ ]
Gambit v4.1.2
> (define-class Point Object (x y))
Point
> (define p (make-Point 0 1))
> (unveil p)
(a Point <------------- [Id: 1]
x: 0
y: 1 end Point)
#t
> (Point-x-set! p 1)
#<meroon #2>
> (unveil p)
(a Point <------------- [Id: 1]
x: 1
y: 1 end Point)
#t
>

Numerical Integration

This first part will be about numerical integration (quadrature rules).
The Gauss-Lobatto quadrature rules with n points have the form

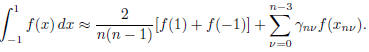
Here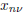 are the zeros of the degree n − 2 orthogonal polynomial over [−1, 1] with the weight

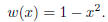
If we define

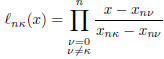
then 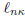has degree n − 1 and satisfies

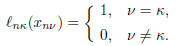
The weights 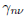satisfy

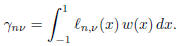
So, the first part of the project is to write code to manipulate polynomials.
and modify it to use Meroon’s framework of classes/objects and generics/methods.

We’ll define a polynomial class:

(define-class Polynomial Object
((= variable immutable:)
(= terms immutable:)))

and a way to check whether two Polynomial variables are the same:

(define (Polynomial-variable= var1 var2)

(eq? var1 var2))

The terms of a polynomial is just a list of nonzero terms, in decreasing order by degree (unfortunately called
“order” at that web page), so we need some code to manipulate terms and lists of terms:

;;; a term is a pair (coeff order) (order should really be degree, but ...)
;;; (Polynomial-terms p) is a list of terms in decreasing orders.
;; operation on terms and term-lists
(define (adjoin-term term term-list)
(if (=zero? (term-coeff term))
term-list
(cons term term-list)))
(define (the-empty-termlist)
’())
(define (first-term term-list)
(car term-list))
(define (rest-terms term-list)
(cdr term-list))
(define (empty-termlist? term-list)
(null? term-list))
(define (make-term order coeff)
(list order coeff))
(define (term-order term)
(car term))
(define (term-coeff term)
(cadr term))

The web page has code for adding two polynomials. Putting it into our terms we define a generic function
add that should work for everything, and we start with it working with numbers:

(define-generic (add (x) y)
(if (and (number? x)
(number? y))
(+ x y)
(error "add: This generic is not defined on these objects: " x y)))

and then we define a method for adding Polynomials:

(define-method (add (p_1 Polynomial) p_2)
(cond ((number? p_2)
(add p1 (number->Polynomial p2 (Polynomial-variable p1))))
((and (Polynomial? p_2)
(Polynomial-variable= (Polynomial-variable p_1)
(Polynomial-variable p_2)))
(instantiate Polynomial
variable: (Polynomial-variable p_1)
terms: (add-terms (Polynomial-terms p_1)
(Polynomial-terms p_2))))
(else
(error "add: p_2 is neither a number nor a polynomial with the same variable as
p_1 " p_1 p_2))))

This method is called only when p_1 is a polynomial; if p_2 is a number, it converts p_2 to a Polynomial
with the same variable as p_1 and calls add again with both arguments now a Polynomial.

The web page has code for add-terms:

(define (add-terms l1 l2)
(cond ((empty-termlist? l1) l2)
((empty-termlist? l2) l1)
(else
(let ((t1 (first-term l1))
(t2 (first-term l2)))
(cond ((> (term-order t1)
(term-order t2))
(adjoin-term t1
(add-terms (rest-terms l1) l2)))
((< (term-order t1)
(term-order t2))
(adjoin-term t1
(add-terms l1 (rest-terms l2))))
(else
(adjoin-term
(make-term (term-order t1)
(add (term-coeff t1)
(term-coeff t2)))
(add-terms (rest-terms l1)
(rest-terms l2)))))))))

So you need to define number->Polynomial, which takes two arguments.

You need to define a multiply generic that works with numbers by default, and a method for multiply
that works on Polynomials; follow ths same pattern as for add. The web page has the guts of the code:
(define (multiply-terms l1 l2)

(if (empty-termlist? l1)
(the-empty-termlist)
(add-terms (multiply-term-by-all-terms (first-term l1) l2)
(multiply-terms (rest-terms l1) l2))))
(define (multiply-term-by-all-terms t1 L)
(if (empty-termlist? L)
(the-empty-termlist)
(let ((t2 (first-term L)))
(adjoin-term
(make-term (+ (term-order t1)
(term-order t2))
(multiply (term-coeff t1)
(term-coeff t2)))
(multiply-term-by-all-terms t1 (rest-terms L))))))

So that’s pretty much the code that comes on the web page. Meroon defines a generic function show
that we can specialize for Polynomials as such:

(define-method (show (p Polynomial) . stream)
(let ((port (if (null? stream)
(current-output-port)
(car stream))))
(if (=zero? p)
(display 0)
(show-terms (Polynomial-variable p)
(Polynomial-terms p)
port))
(newline port)))
(define (show-terms variable terms port)
(show-first-term variable (first-term terms) port)
(for-each (lambda (term)
(show-term variable term port))
(rest-terms terms)))
(define (show-first-term variable term port)
(let ((coeff (term-coeff term))
(order (term-order term)))
(display (list (if (and (= coeff 1)
( positive ? order))
’()
coeff)
(cond ((zero? order)’())
((= order 1) variable)
(else
(list variable "^" order)))))))
(define (show-term variable term port)
(let ((coeff (term-coeff term))
(order (term-order term)))
(display (list (if ( negative ? coeff)
coeff
(list "+" coeff))
(cond ((zero? order)’())
((= order 1) variable)
(else
(list variable "^" order))))
port)))

It will probably help your debugging.

So, here are some problems.
(1) The above code uses a function =zero?. Define a generic function =zero? that handles numbers.
Define a method that works with Polynomials.

(2) Define a generic function (negate (x)) that handles numbers by default. Define a method for
negate that works with Polynomials. Use the generic negate to define a regular function ( subtract
x y).

(3) Define a function ( exponentiate x n ) that uses multiply to exponentiate anything that multiply
can multiply. Use the discussion of exponentiation on page
as your model.

(4) Define a function (variable->Polynomial x) that takes a symbol x and returns a Polynomial that
represents the polynomial x, i.e., a single term with coefficient 1 and order 1.

(5) Define a generic function (evaluate f x) that evaluates the function f at x. If f is a number,
assume that it means a function that constantly returns f. Define a method for Polynomials.

If you’ve done the exercises until now, something like the following should work.
;;; evaluation
(define-generic (evaluate (f) x)
(if (number? f)
f
(error "evaluate: unknown argument types " f x)))
(define-method (evaluate (p Polynomial) x)
(evaluate-terms (Polynomial-terms p) x))
(define (evaluate-terms terms x)
(if (empty-termlist? terms)
0
(add (evaluate-term (first-term terms) x)
(evaluate-terms (rest-terms terms) x))))
(define (evaluate-term term x)
(multiply (exponentiate x (term-order term))
(term-coeff term)))

Can you write a method that uses Horner’s rule for evaluating Polynomials in our representation?