Solving Quadratic Equations

Warm-up
Evaluate each expression if a = 6, b = -2, and c = 12.

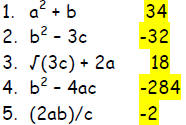
Today we will:
1. Solve problems about situations modeled by parabolas . Last section in the
book!

Following class period we will:
1. Review key concepts

10-8 Solving Quadratic Equations
o Quadratic equation – an equation that can written in the form an equation
0 = ax² + bx + c, where a, b, and c are numbers and a ≠ 0.

o Quadratic formula – the formula is used to find the solutions of a
quadratic equation.

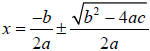
Today we will solve the quadratic equations by…
• Graphing (the x- intercepts are the solutions )
• Using the quadratic formula

Solving 0 = ax² + bx + c by graphing
The solutions to 0 = ax² + bx + c are the x-intercepts of the graph of the
equation y = ax²+ bx + c.

One way to solve is by drawing an accurate graph. If the graph doesn’t cross
the x-axis at points that correspond to integral units on the grid, the solutions
will be approximations.

Example 1:
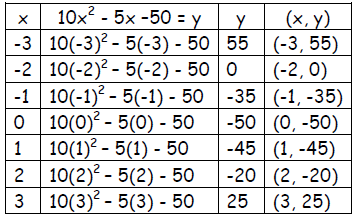
Solve 10x² - 5x –50 = 0 by graphing

Solution - Graph the quadratic function 10x² - 5x –50 = y
Step 1 – Make a table of values.

Step 2 – Use the table to draw a graph

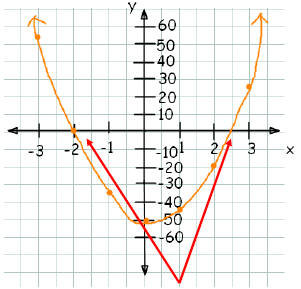
Step 3 – Read the x-intercepts from the graph.
The x-intercepts are at –2 and 2.5,
so the solutions of 10x² - 5x –50 = 0 are x = -2 and x = 2.5.

Check your solution. Substitute –2 and 2.5 into the original equation.

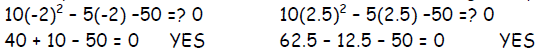
Using the quadratic formula to solve ax²+ bx + c = 0

Unlike graphing where approximate solutions may be necessary, the quadratic
formula gives exact solutions to any equation ax²+ bx + c = 0.

Often the solutions involve square roots of numbers that are not perfect
squares. In such cases, you can approximate the solutions or give the exact
solutions in square root form .

Example 2:
Use the quadratic formula to solve 2x²+ 5x = 25

Solution
Step 1 - Write the equation in the form ax²+ bx + c = 0 and determine the
values of a , b, and c.

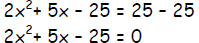
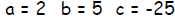
Step 2 – Use the quadratic formula.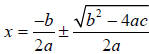

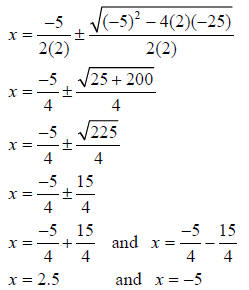
Check your solutions – substitute 2.5 and –5 in the original equation.

Example 3:
Use the quadratic formula to solve 0 = x² - 11x + 18

Solution
Step 1 - Determine the values of a, b, and c.

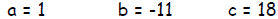
Step 2 – Use the quadratic formula.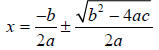

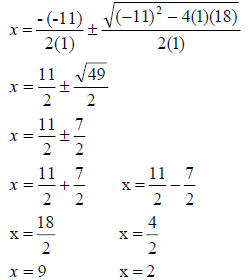
Check your solutions – substitute 9 and 2 in the original equation.
Yep, both work!

In Summary …
To solve quadratic equations we can…
• Graph to find the x-intercepts
• Use the quadratic formula
• Factor ( and use the Zero - Product Property )