Problem: Show that a real number q is rational if
and only if there are three distinct
integers,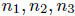 
, such that
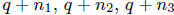forms a geometric progression.
Solution (by Richard B. Eden, Math. Graduate student, Purdue)
Suppose q is a rational number . If q = 0, we can choose
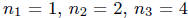. So now
suppose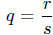 
, not necessarily in lowest terms ,
where r, s ∈ Z, s ≠ 0 and r ≠ 0. We can
also assume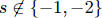 
since we can multiply r and s by
the same constant.
Let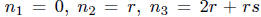 
. These three integers are distinct since
r ≠ 0 and
s ≠ -1,-2. In this case,
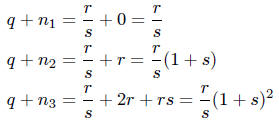
really do form a geometric sequence.
Now suppose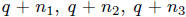 
form a geometric sequence with
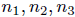distinct
integers. This means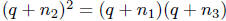 
, which implies
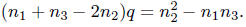
If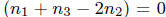 
, so
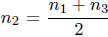, we can write
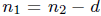and 
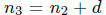for
some d ∈ Z. We then have, from the above equation ,
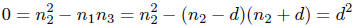
so d = 0 and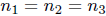 
. However,
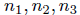are all distinct. Therefore,
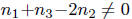
and
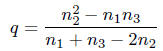
which is a rational number .
Also solved by :
Undergraduates: Noah Blach (Fr. Math ), Nathan Claus (Fr.
Math)
Graduates: Miguel Hurtado (ECE)
Others: Brian Bradie (Christopher Newport U. VA), Hoan Duong (San Antonio
College),
Elie Ghosn (Montreal, Quebec), Brian Huang (Jr. Saint Joseph's HS, IN), Gerard
D.
Ko & Swami Iyer (U. Massachusetts, Boston), Steven Landy (IUPUI Physics), Sorin
Rubinstein (TAU faculty, Israel), Steve Spindler (Chicago), Kevin Ventullo (IIT,
Chicago)
