Prerequisite: Math 6099 or its equivalent.
The topics covered in Math 6099 are : Real number system , properties of
exponents
and radicals, algebraic expressions, operation on polynomials, solving linear
equations, rectangular coordinate system , lines, and complex numbers. These
topics
are also covered in Chapter 1 of your textbook.
Rationale: Precalculus for science majors is a one semester course which is a
prerequisite for the calculus sequence. The focus of this course are
functions and
graphs- linear, quadratic, polynomial, rational, exponential, logarithmic, and
trigonometric-analytic trigonometry, and solving systems of two equations in two
variables. Students learn graphing skills and techniques which are not only
necessary for the calculus sequence but also for other science courses.
Course Goals: This course provides students with an understanding of the
concepts
of functions and graphs. With the aid of the TI-83, students will learn
different
graphing techniques. Students will also learn to prove trigonometry identities
and
to solve systems of equations in two variables. The course will also help
students to
develop an appreciation for mathematics and to realize its importance to
society.
Course Objectives: Students will be able to:
Functions (2.1-2.2, 2.4-2.5)
1. Identify functions.
2. Explain why a given relation is not a function.
3 Evaluate functions for given values of the independent variable.
4. Sketch the graph of each of the following basic functions-identity, square,
cubic,
square root , reciprocal, absolute value.
5. Graph any given function using transformation and other graphing techniques.
6. Operate on functions- add , subtract , multiply, divide, and compose.
7. Determine if a function is one-to-one.
8. Explain why a function is/is not invertible.
9. Find the inverse of a function.
10. Sketch the graph of an inverse function.
11. Find the domain and range of a function and its inverse.
12. Prove/disprove that two functions are/are not inverses of each other.
Quadratic Functions (2.3)
13. Find the equation of a parabola-either standard or general form.
14. Sketch the graph of a quadratic function/ parabola using transformation
techniques.
15. Solve quadratic equations/functions either graphically-with the aid of the
TI-83-
or algebraically.
16. Solve story problems involving quadratic equations.
Polynomial Functions (3.1-3.4)
17. Sketch the graph of a polynomial function of degree greater than 2.
18. Identify intervals of the real line where a given polynomial function is
greater
than or less than zero.
19. Divide polynomials using long division or synthetic division .
20. Find the real, complex , and rational zeros of polynomial functions.
Rational Functions (3.5)
21. Identify the vertical, horizontal, or oblique asymptote of rational
functions.
22. Sketch the graph of a rational function.
Exponential Functions (4.1-4.2)
23. Sketch the graph of exponential functions.
24. Solve problems involving exponential equations.
Logarithmic Functions (4.3-4.5)
25. Sketch the graph of logarithmic functions.
26. Solve problems involving logarithmic equations.
Solving Systems of Equations (8.1-8.2)
27. Solve systems of two equations in two variables using the substitution
method or
the method of elimination .
Trigonometric Functions (5.1-5.6)
28. Convert degrees to radians and radians to degrees.
29. Sketch the graph of trigonometric functions-sine, cosine, tangent, cosecant,
secant, and cotangent.
30. Identify the amplitude (where applicable), period, and phase shift of
trigonometric functions.
31. Solve problems using the definition of trigonometric functions of an angle
of a
Right Triangle.
Analytic Trigonometry (6.1-6.3, 6.6)
32. Verify trigonometric identities using the fundamental
identities-Pythagorean,
reciprocal, tangent, and cotangent.
33. Solve trigonometric equations.
34. Sketch the graph of the inverse sine, cosine, and tangent functions
General Methodology: Lecture /Discussion /Demonstration /Cooperative
activitiessmall
groups /Problem solving
Accommodation for Students With Special Needs: If
you have a disability for which
you are or may be requesting an accommodation, you are encouraged to contact
both
your instructor and the Academic Success Center’s Disability Resources and
Services
Office (Hanley Library, Room 218). Contact Kara Kennedy, Learning Development
Specialist, at 362-7609 for more information.
Expectations:
1. I intend to treat each student with respect and I therefore expect each
student to be
respectful to myself and to every other member of the class.
2. You should try to attend all classes. If you have to miss a class due to some
uncontrollable circumstance, it is your responsibility to find out what material
was
covered during that missed class and what assignments were distributed .
3. You are expected to devote about 12 hours weekly, besides the 4 in-class
hours, to this course.
4. You are supposed to be active participants in the group work in order to
receive the 25 points for class participation.
5. You may collaborate on the take-home quizzes but the work you submit must
be your own understanding of the concepts since you will not be able to
collaborate on your in-class exams.
Evaluation:
1. Scheduled Exams - (3 @ 75 points each - 225 points total). The dates for the
exams
are listed in the course outline.
2. Take-home Quizzes - (10 @ 15 points each – 150 points total).
More than 10 quizzes will be given throughout the semester but only your best 10
quizzes
will count towards your final grade. They will be based on reading assignments,
practice
problems and worksheet problems.
3. Final exam -100 points. The date and time for your final exam are listed in
the course
outline.
4. Class participation -25 points.
Total Number of Points: 500
Quizzes-30 % of overall grade
Exams -65% (Exam #1, 2, and 3 15% each and final exam-20%)
Class participation-5%
Letter grades will be assigned according to the following
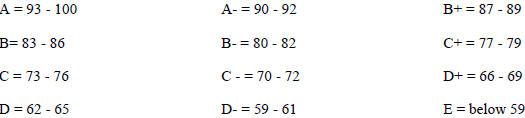 |



