Order of Operations
Definition: The order in which the operations of a calculation must be
completed.
Perform operations in the following order:
Parentheses: Any operations contained in parentheses ( ), brackets [ ],
and braces { }are
done first, if there are any.
Exponents: Exponents and roots are simplified second, if there are any.
Multiplication and Division: These operations are done next in the
order in which they
are found, going left to right; that is, if division comes first going left to
right, then it is
done first.
Addition and Subtraction: These operations are done next in the
order in which they
are found going left to right; that is, if subtraction comes first, going left
to tight, then it is
done first.
Example: simplify
|
 |
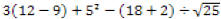
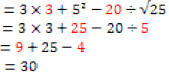Complete operations in parentheses first
Next, complete exponents & roots
Next, complete multiplications & divisions as they occur from left to
right
Finally, complete additions & subtractions as they occur from left to
right
|
DECIMAL NUMBERS
The place value of each digit in a base ten number is determined by its position
with respect to
the decimal point. Each position represents multiplication by a power of ten.
Example: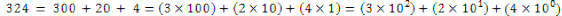 
Example: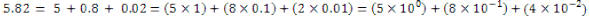 
Example: Identify the place value of each digit in 123.456. 1 is the
hundreds place, 2 is the tens
place, 3 is the ones or units place, 4 is the tenths place, 5 is in the
hundredths place, 6 is in the
thousandths place.
Writing Decimal Numbers as Fractions
Write the digits that are to the right of the decimal point as the numerator
(top) of the
fraction
Write the place value of the last digit as the denominator (bottom) of the
fraction.
Any digits to the left of the decimal point are whole numbers
Example: In 4.67, the last digit to the right of the decimal point is 7
and it is in the hundredths
(100ths) place; therefore,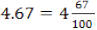 
Notice the number of zeros in the denominator is equal to the number of digits
to the right of the
decimal point in the original number.
Addition of Decimal Numbers
Write the decimal numbers in a vertical form with the decimal points lined up
one under
the other, so digits of equal place value are under each other.
Example: Add: 234.67 + 45.458
 |
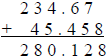Addend |
|
Addend |
|
Sum |
Subtraction of Decimal Numbers
Write the decimal numbers in a vertical form with the decimal points lined up
one under
the other.
Write additional zeros to the right of the last digit in the minuend (number on
top) if
needed ,both the minuend and the subtrahend should have an equal number of
digits to
the right of the decimal point.
Example: Subtract: 346.34 – 97.452
 |
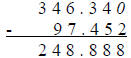Minuend |
|
Subtrahend |
|
Difference |
Multiplication of Decimal Numbers
Multiply the factors as if they were whole numbers.
Find the total number of digits to the right of the decimal point in all
factors.
Count that many places from the right end of the product , then insert a decimal
point. It
is not necessary to line the decimal points up in multiplication.
Example: Multiply: 12.89 × 3.2
 |
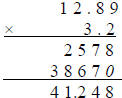(2 digits to the right of decimal point) |
|
(1 digit to the right of decimal point) |
| |
| |
|
(Count 3 places from the right end, insert decimal point) |
RATIO, PROPORTION , & PERCENT
Ratio
Definition: Comparison between two quantities written as a quotient.
Examples: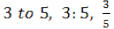 
Proportion
Definition: Statement of equality between two ratios.
Examples: 3/6 = 6/12, 3 : 6 :: 6 : 12, 3 is to 6 as 6 is to 12
Percents
Definition: Percent means out of 100 or per 100
Changing Percents into Fractions: Percents can be written as fractions by
placing the
number over 100 and simplifying or reducing.
Example: 20% = 20/100 = 2/10 ; 4.5% =4.5/100 = 45/1000 = 9/200
Changing Fractions into Percents: Write the fractions with a denominators of
100. The
numerator is then the percent number.
Example: 3/5 = 3/5 x 20/20 = 60/100 = 60%
Changing Percents into Decimal: Move the decimal point two places to the left,
remove
% sign
Example: 25% = 0.25
Changing a Decimal into a Percent: Move the decimal point two places to the
right, add % sign
Example: 4.89 = 489%
FRACTIONS
Reducing
Divide the numerator (top) and the denominator (bottom) by the same number,
thereby making
an equivalent fraction in lower terms.
Example: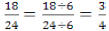
Addition & Subtraction
Same denominators: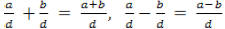 
where d≠0
Example: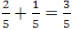 
Example: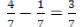 
Different denominators :
1) Find the least common denominator by determining the smallest number
which can be divided evenly (no remainders)by all of the denominators .
2) Multiply the numerator and denominator of each fraction to make equivalent
fractions with the common denominator.
3) Add the numerators and over the common denominator.
Example: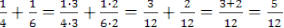 
Example: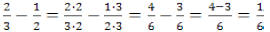
Multiplication
Multiply the numerators then multiply the denominators. To finish, reduce the
fraction to
lowest terms, if necessary. Common denominators are not needed.
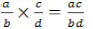
Example: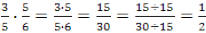 
Division
Flip the fraction to the right of the division sign and change the division sign
to a
multiplication sign.
Multiply the numerators then multiply the denominators. To finish, reduce the
fraction to
lowest terms, if necessary. Common denominators are not needed.
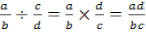
Example: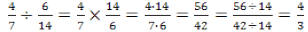 
ALGEBRA
Vocabulary
Variables are letters used to represent numbers.
Constants are specific numbers that are not multiplied by any variables.
Coefficients are numbers that are multiplied by one or more variables.
Terms are constants or variable expressions.
Like or similar terms are terms that have the same variables to the same degree
or
exponent value. Coefficients do not matter, they may be equal or not.
Polynomials are terms that are connected by either addition or
subtraction.
Equations are statements of equality between at least two terms .
