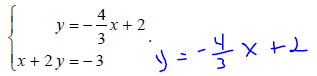Definition
A solution to a system of two linear equations with two
unknowns is an ordered pair that makes each of
the equations true .
Examples
Decide whether or not the given ordered pairs are
solutions to the system of equations:
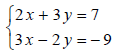
Is (5,−1) a solution to the system ?
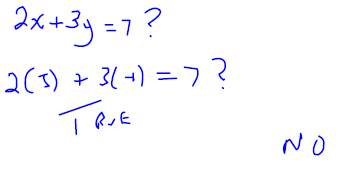
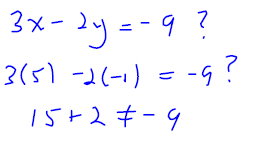
Is (−1,3) a solution to the system?
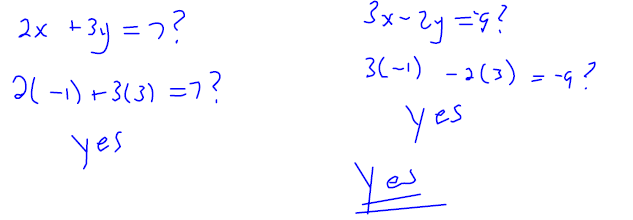
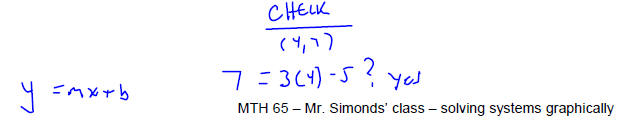
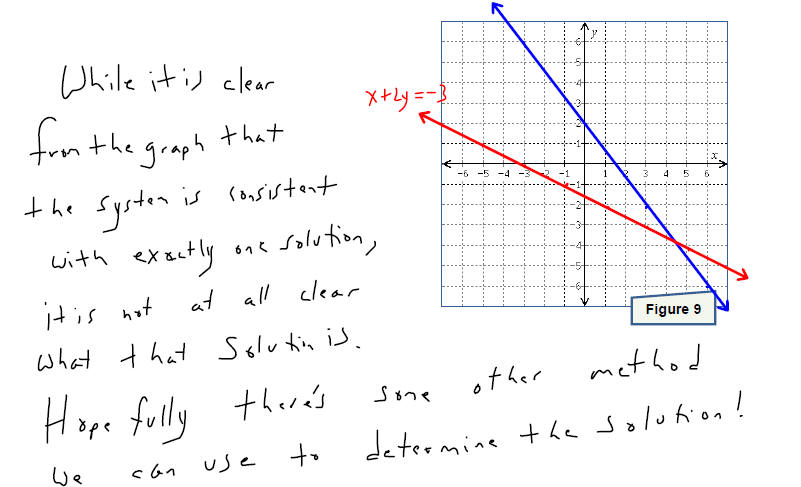
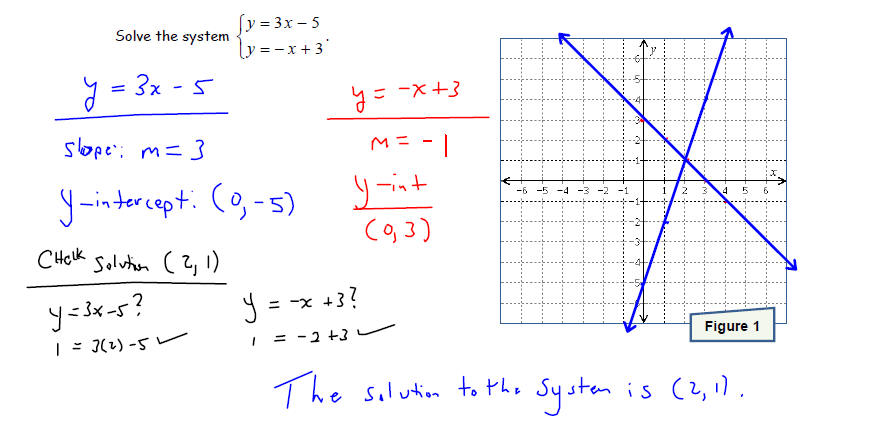
Solve each system of equations by graphing the two linear
equations and finding the point(s) they
have in common . Make sure that you check your solution before stating your
conclusion.

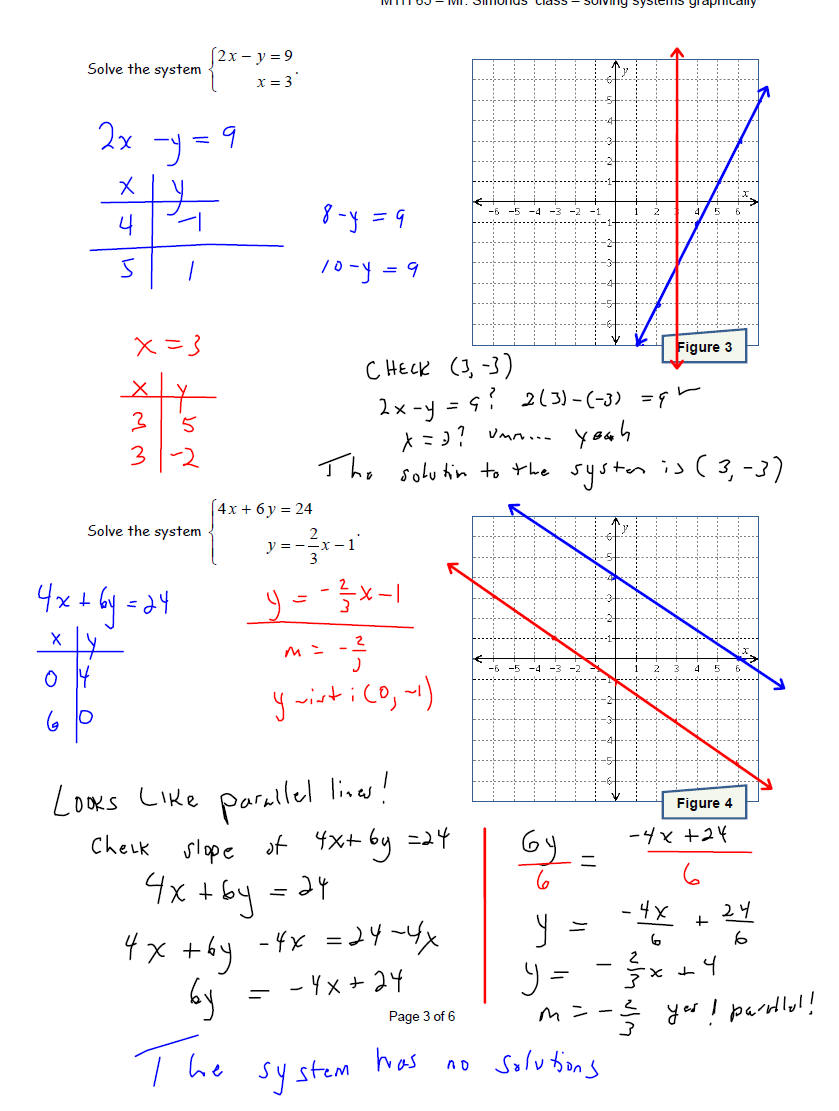
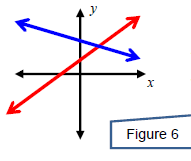
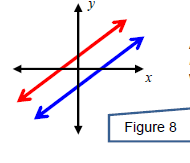
A system can have exactly one solution. In this case, the
system is called
consistent and the equations are called independent. This happens
x when the two equations graph to lines that intersect at a single point.
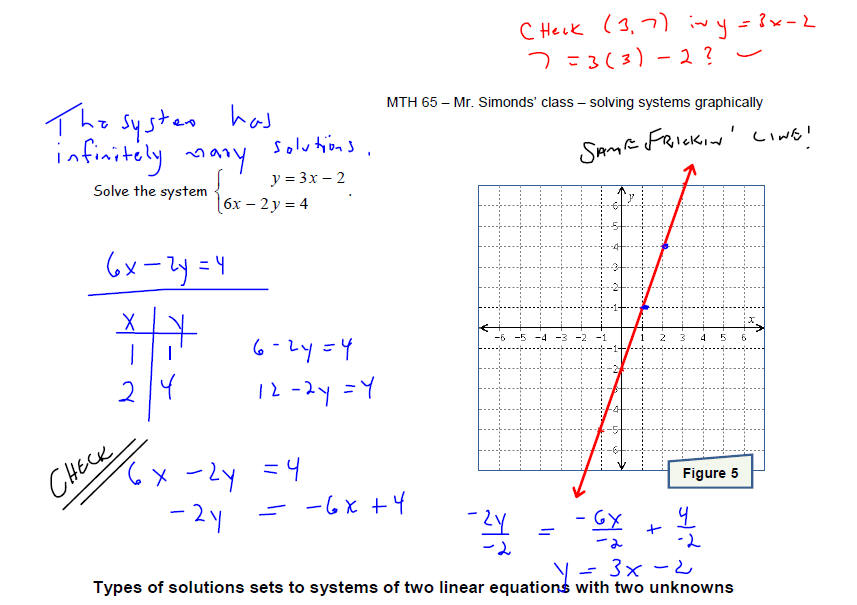
A system can have an “ infinite number ” of solutions. In
this case, the
system is called consistent and the equations are called dependent.
x This happens when the two equations graph to the same line
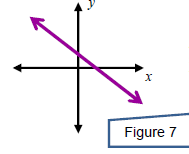
A system can have no solution. In this case, the system is
called
inconsistent and the equations are called independent. This
happens
x when the two equations graph to parallel lines .
Examples
For each system, write both equations in
slope - intercept form and decide – without graphing –
whether the system is consistent or inconsistent and whether the equations are
dependent or


Find the solution to the system of equations