Due 5/19/09 before the final. The following questions are
similar to some of those you will
encounter on the final. Complete and show your work on a seperate sheet of
paper.
REMARK 1. This review sheet is a guideline and a starting point, it is
expected that you also
review all past exams and exam reviews.
1. Chapter 1 - Order of operations , rules of exponents, simplifying exponents,
scientific notation.
See also review for exam 1.
(a) Evaluate the following:
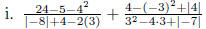
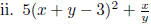when x = 9, y = -3.
(b) Simplify and write the answer without a negative exponent :
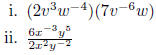
2. Chapter 2 - Solve linear equations , problem solving
(word problems), linear inequalities, abso-
lute values.
(a) Solve the linear equations or inequalities:
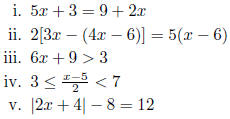
3. Chapter 3 - Understand functions and graphing, graphing
lines, slope, slope-intercept form,
point- slope form , graphing linear inequalities.
(a) Know how to use the vertical line test. (See problem 1 from exam 2 review).
(b) For the functions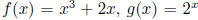 
, evaluate
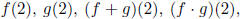
(f/g)(2)
(c) Equations of lines :
i. Find the x- and y-intercept of 2x - 3y = 12, graph the line.
ii. Find the slope and y-intercept of 5x + 15y = 30, graph the line.
iii. Find an equation of the line that passes through the points (1, 3) and (2,
-1).
(d) Linear Inequalities : Graph 3x - 4y≤ 12
4. Chapter 4 - Solving systems of linear equations in two variables, matrix
notation, Cramer's
Rule
(a) Solve systems of equations:
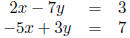
(b) Solve the system of equations using Cramer' s rule :
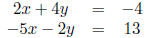
5. Chapter 5 - Polynomials : addition, subtraction,
multiplication, division, factoring.
(a) Multiply and simplify completely: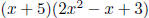 
(b) Divide using long division: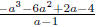
(c) Factor :
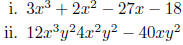
6. Chapter 6 - Domains of rational functions,
multiplication, division, addition and subtraction
of rational functions, finding LCD, solving rational equations.
(a) Multiply or divide, simplify completely: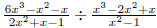
(b) Find the LCD and add or subtract, simplify completely: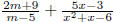
(c) Solve, remember to check your solutions: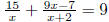
7. Chapter 7 - Rational exponents, simplifying radicals,
add, subtract, multiply, and divide rad-
icals, solve radical equations.
(a) Simplify:
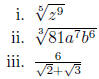
(b) Solve: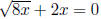
8. Chapter 8 - Completing the square , quadratic formula,
quadratic form (substitution), graph
quadratic functions.
(a) Solve by completing the square: x2 + 10x = 11
(b) Solve using the quadratic formula : (2a + 3)(3a - 1) = 2
(c) Graph, label the vertex , y-intercept, and x-intercepts if any: f(x) = -x2
- 2x + 24
9. Chapter 9 - Composition and inverse of functions, graph exponential
functions , definition and
properties of logarithm , common logarithms, solving exponential equations.
(a) If f(x) = 3x + 3 and g(x) = 2x + 5, find (f o g)(x)
(b) If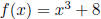 
find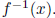 
(c) Graph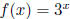 
(d) Write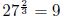 
in logarithmic form
(e) Write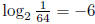 
in exponential form.
(f) Solve the equation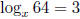 
for x.
(g) Expand using the properties of logarithms:
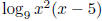
(h) Write as a single logarithm: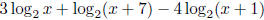 
(i) Solve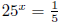 
10. Word Problems - Know how to set up and solve the following application
problems: Section
2.3 # 29; Section 2.4 # 1, 11; Section 4.3 # 5; Section 8.5 # 73, 99
