The exam will cover sections 5.1-5.6. This review also
includes sections 4.5-4.6, for the final exam.
Section 5.1 Composite Functions
Some functions are constructed in several steps, where each of the individual
steps is a function . For example,
you would evaluate h(x) = (2x + 3)4 by first computing g(x) = 2x + 3 and then
raising it to the 4th power.
This is expressed mathematically by writing h(x) = f(g(x)), where g(x) = 2x + 3
and f(x) = x4. Here one
formula is substituted into another, giving a composite function.
See page 392 for the definition of a composite function, see page 396 for an
important application.
To find the domain of a composite function f(g(x)), start with the domain of g(x).
(The domain of
f(g(x)) is always contained in the domain of g.) Then, depending on the formula
you get for f(g(x)), you
might need to exclude some more values. Review questions: p397 #11,19,33,41,61
Section 5.2 Inverse Functions
The inverse of a function is like a \reverse look-up" function. Usually we use a
formula y = f(x) to nd
y when x is given. What about the reverse? Given y, how can you find x? This is
the job of the inverse
function. To give a definition of an inverse function, we use the notion of a
composite function.
The function g(x) is the inverse of f(x) if f(g(x)) = x and g(f(x)) = x, for all
x. These equations say
that g does exactly reverse of f. A good example to think of is
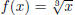and g(x) = x3.
When g is the inverse of f, we usually write g = f -1, and read this as \g equals
f inverse". See the last
box on page 403 for the basic relationship used to define of f -1:
f-1(f(x)) = x and f(f-1(x)) = x :
Not all functions have an inverse function. If two x -values produce the same
y-value in the formula
y = f(x), then given y there is no unique way to recover x. In order to have an
inverse, the graph of
y = f(x) must pass the horizontal line test (see page 402). If y = f(x) passes
the test, then we simply
interchange x and y in the formula y = f(x), and solve for y to get the formula
for the inverse. See the
bottom of page 406 for this procedure for actually find the formula for the
inverse of a function.
A function and its inverse are closely connected. The domain of f -1 is the range
of f, the range of f -1
is the domain of f (see page 403). The graph of f -1 is the mirror image of the
graph of f, in the line y = x.
This happens since if the point (x, y) is on the graph of f, then the symmetric
point (y, x) must be on the
graph of f -1 (see page 405). Review questions: p410 #25,33,37,41,49,65
Section 5.3 Exponential Functions
An exponential function is one of the form
f(x) = ax
where a is a positive real number and a ≠ 1. (We will usually assume that a >
1.) The domain of an
exponential function is the set of all real numbers. Its graph has the x-axis as
a horizontal asymptote. The
points (0, 1), (1, a), and (-1, 1/a) are easy ones to plot. Note that if x
increases by 1, then f(x) is multiplied
by a, since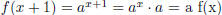 
(see the top of page 415).
You need to be familiar with the basic shape of an exponential function. See
Figure 13 on page 415 for
the graph of y = 2x and Figure 22 on page 420 for the graph of y = ex. The base
e is important because it
makes calculations easier when doing calculus. (It is the one exponential
function whose graph crosses the
y-axis at a 45 degree angle, making the slope of the graph equal to 1 when x =
0.) For our class, the only
thing you need to remember about e is its approximate value of 2.7 and the fact
that the graph of y = ex
lies between the graphs of y = 2x and y = 3x.
Building on the basic shape of y = ax, we can graph other functions in the
family by using transformations
(as we did in Section 3.5). Sample questions: p424 #21,25,39,49,55,5973
A logarithmic function (or log function for short) is one
of the form
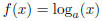
where a > 0 and a ≠ 1. If a = 10, we usually write log(x) instead of
.
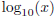If a = e, we write ln(x)
instead of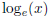 
, and call this the natural log function.
The log function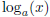 
is defined to be the inverse of the exponential function
ax. First, this tells us
the basic shape of the graph (see Figure 25 on page 431). It also guarantees
that the graph has the y-axis
as a vertical asymptote, and that the domain of
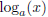is (0,+∞), the same as
the range of ax. Now, when
finding the domain of a function, you not only need to watch out for division by
zero, or the square root of
a negative number , but also for the log of a negative number. All of these are
undefined for real numbers.
To express the inverse relationship, we can say that
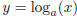if and only if
x = ay (see the top of page
429). We also have the following equations, which summarize the inverse
relationship (see the theorem on
page 442):
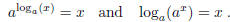
These identities are important in solving equations that involve logs. For
example, to solve the equation
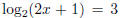we need to simplify the left hand side. Since
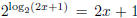, the first step is to
make both sides of the equation into an exponent with base 2, to get
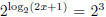, which simplifies to
2x + 1 = 8. To solve the equation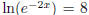 
, just note that the left hand
side is equal to -2x, so the
equation simplifies immediately to -2x = 8. To solve the equation
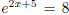, we
need to get rid of the
base e on the left hand side. This is done by substituting both sides into the
natural log function, to get
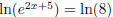, or simply 2x + 5 = ln 8. Review questions: p438
#25,41,45,51,67,83,89,93,105
Section 5.5 Properties of Logarithms
Since logs represent exponents, they should behave like exponents. For example,
if we write two numbers M
and N in scientific notation as powers of 10, then to multiply M and N we only
need to add the exponents .
To find the square root of M, we only need to divide the exponent of M by 2. The
crucial properties of logs
are summarized in the following equations (see page 443).
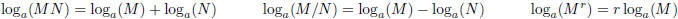
There is also a formula to change the base :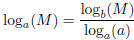 
. (See the summary on page 448.)
Review questions: p449 #13,17,29,41,49,57,81,83
Section 5.6 Log and exponential equations
In this section, the properties of logarithms are used to solve various kinds of
equations.
Review questions: p454 #9,17,31,37,41
Review for the final exam
Section 4.5 Polynomial and Rational Inequalities
The method of solution is given on page 357. In terms of the graph of a
polynomial or rational function, we
need to determine when the graph is above or below the x-axis. We first decide
where the graph can change
from positive to negative , and from negative to positive. Then if we know that
we have found an interval
on which the graph cannot change sign, it is enough to test one point in the
interval. Just be very careful
in working these problems. Review questions: p361 #5,11,21,35,43
Section 4.6 Zeros of a Polynomial
You are only responsible for pages 362-365 of this section. This involves the
division algorithm, the remainder
theorem, and the factor theorem . The factor theorem is important because it says
that roots of a polynomial
equation correspond exactly to linear factors of the polynomial. If f(x) is a
polynomial, and you know that
f(c) = 0, then you are guaranteed that x-c is a factor of f(x). If you don't see
the other factor right away,
you can always use the division algorithm to find it. Review questions: p375
#3,13,19
