Math Final Exam Reference Sheet

Distance between two points

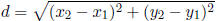
Midpoint between two points

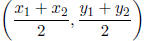
Slope between two points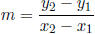

Average rate of change of a function

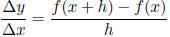
Inverse functions

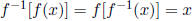
Transformations of graph of f(x)

f(x − h) + k translates h units ”to the right”,
and k units vertically

−f(x) reflects across x−axis; f(−x) across y−
cf(x) dilates by factor of c vertically
f(cx) dilates by factor of 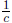horizontally

Polynomials

General Form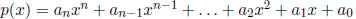
Factored Form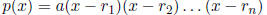
Roots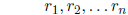

Rational Functions

Definition 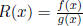where f, g are polynomials with no common factors
Domain all real numbers except where g(x) = 0
x- intercepts at zeros of f
vertical asymptotes at zeros of g

Exponents and Logarithms
Exponential Function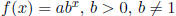
Definition of Logarithm 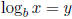is equivalent to b^y = x
Properties of Logs


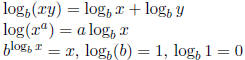
Trigonometric Functions
Of acute angles: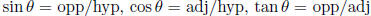
Of any angle: 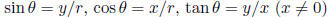( circle radius r)

Radians and Degrees 180° =π (radians)

Linear equations

General Form: Ax + By =C
Slope-intercept form y = mx + b
Point-slope form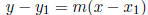
Double-intercept form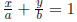

Quadratic equations

Forms:	General
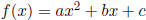	Vertex
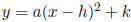	Factored
Vertex	General
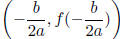	Vertex
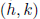	Factored
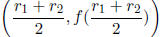Roots	General
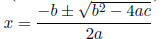	Vertex
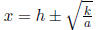	Factored

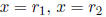Translations, Reflections, Dilations y = Asin(B(x − C)) + D, y = Acos(B(x − C)) + D
Horizontal Translation (phase shift) C units
Vertical Translation (vertical shift) D units
Horizontal Dilation By a factor of 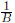(period becomes )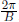
Vertical Dilation (amplitude) By a factor of A
Reflections −f(x) reflect across y−axis; f(−x) reflect across x−axis

Trig Identities
Definitions
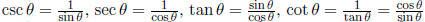
Pythagorean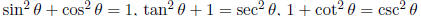
Opposite Angle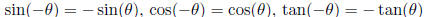
Periodicity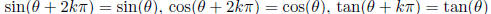
Complements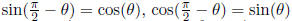
Reduction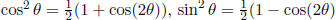
Addition

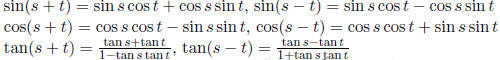
Double-Angle

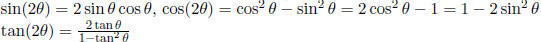
Half-Angle s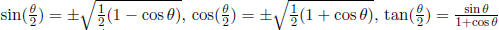
Product-to- Sum

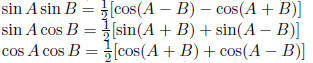
Sum-to-Product

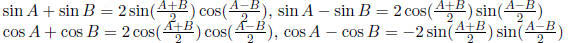
Inverse Trig Functions
Domain restrictions: sin restr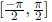icts to , cos restricts to [0,π ], tan restricts to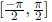
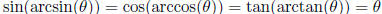for all θ

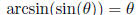only for
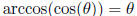only for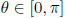
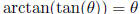only for

Vectors
Position(radius) Given 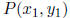and
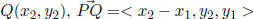
Unit Components If 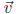=< x, y >, then
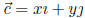
Magnitude (length) If 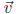=< x, y >, then 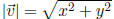Unit vector
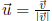
Scalar Multiplication If 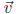=< x, y >, then k 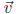=< kx, ky >
Addition If 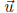=< a, b > and 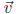=< c, d > then 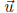+ 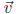=< a + c, b + d >
Dot Product If 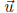=< a, b > and 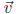=< c, d > then 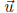· 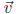= ac + bd
Angle between 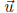and

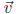
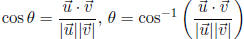
Polar Coordinates

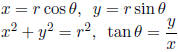
Trigonometric (polar) form of Complex Numbers
z = r(cosθ + i sinθ ) is the trigonometric form of the complex number a + bi, where
a = r cosθ , b = r sinθ and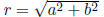
zn = rⁿ(cos nθ + i sin nθ ) with z as above

Matrices
Matrix Multiplication If 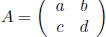and 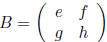, then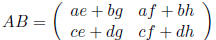
Identity Matrix 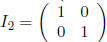. For any 2 × n matrix A,
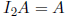
Inverse Matrices 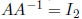and
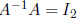
Matrix equations If AX = B, then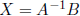
Determinants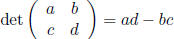

Polynomial Functions and Equations
Division Algorithm
Let p(x) and d(x) be polynomials, and assume that d(x) is not the zero polynomial. Then there
are unique polynomials q(x) and R(x) such that p(x) = d(x) · q(x) + R(x), where the degree of
R is less than the degree of d. R(x) is called the remainder.
Remainder Theorem
When a polynomial f(x) is divided by x − r, the remainder is f(r).
Factor Theorem
Let f(x) be a polynomial. If f(r) = 0, then x − r is a factor of f(x). Conversely, if x − r is a
factor of f(x), then f(r) = 0.
Linear Factors Theorem
Any polynomial f(x) of degree n can be be expressed as a product of n linear factors, f(x) =
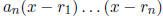, where each 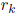is a root of f (x), and may be a real or complex number.
Some roots may be repeated.
Rational Roots Theorem
If 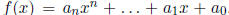, and all the coefficients are integers. Then any root of the
equation f(x) = 0 must be of the form 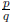, where p is a factor of 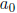(the constant term of f ) and
q is a factor of 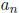(the leading coefficient of f), and p and q have no common factors (so 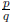is in
lowest terms).
Complex Conjugate Roots Theorem
Let f(x) be a polynomial whose coefficients are real numbers. If a + bi is a root of f(x) = 0,
and b ≠ 0, then a − bi is also a root of f(x) = 0).
Linear and Quadratic Factors Theorem
Any polynomial with real roots can be factored into linear and quadratic factors with real coefficients.

Partial Fractions Decompositions

In the following, we always assume the degree of p(x) is smaller than the degree on the bottom:

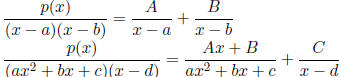,where ax² + bx + c is irreducible

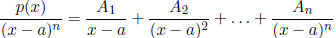
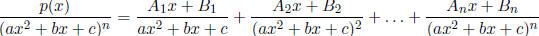,where ax² + bx + c
is irreducible