Mapping with Vectors

Paiute Monument in Inyo Mountains

A. Where in Owen’s Valley Are You ? (Using Polar Coordinates)
You’ve had a typical geologist’s hard night out hiking and camping in Owen’s valley. You wake
up the next morning a little worse for the wear and can’t seem to remember where you are and
what you are doing. You’re not concerned, however, because you have acquired excellent
vector mapping skills at CSUN and know that by siting a few land marks you will soon clear
up your confusion. You find a map for Independence, Ca. on a bench and assume you must be
somewhere within this general vacinity. Use a couple of nearby landmarks to determine your
location and figure out what you are doing.

1. Landmark (A): Off in the distance you can spot one of the tallest peaks near Waucabo
Canyon (elevation 10960) in the Inyo Mountains. You have a Brunton compass with you and
can find true North and East. You can’t determine the actual distance but you can use your
compass to determine that this tall peak is about N77°E. Go to your map and draw a line
(please use photo copy and don’t draw on original maps) through this peak with this azimuth.
You don’t know the distance, so draw the line through this point across your entire map.

2. Landmark (B): Looking in another direction, you can see Paiute Monument (also in the
Inyo Mountains). Using your compass you determine that this is approximately E33°S of you.
Still you don’t know the distance. But you can use the azimuth. Draw a line (please use
photocopy) through the location of Paiute Monument with this azimuth. Again - extend your
line across the map as far as you can. Where this line crosses that line you drew in #1 is your
location! Give your location in latitude and longitude and determine what you are doing there.
(Show your work on the map and turn this in)

B. Where in Owen’s Valley Are You ? (Using Cartesian Coordinates)
After a few days of doing whatever it is you are doing at your present location , you decided to
head towards the Inyo mountains for some recreation. After a days hiking and evening
celebrating, unfortunately, you wake up again unaware of where you are. As you’ve had a
pretty tough time thus far, you decide not to use the polar coordinate method but to try using
the more familiar Cartesian coordinate method to find your location. Find your location and
determine what you are doing now.

3. Think of your unknown location as the origin of a coordinate system where the y and x
axes go through your location. Assume the x axis in due east and the y axis is due north. You
will use the same 2 landmarks on your map as they are still in site. First look at your map and
find the location of your land marks from the western and southern edge of your map. Label
each of these measurements x_a and y_a for landmark A. Label x_b and y_b for landmark B. (You
must use the edges of your map, because you are at the origin of your coordinate system but
you don’t know where you are yet!). When using this method, you can just make these
measurements in centimeters on your ruler (or as actual distance on the map - but this is not
necessary) - just be consistent! Note the error in your measurements.

4. From your new location, your compass tells you that the azimuth to landmark A is N58°E
and landmark B is E55°S of you. Think about the distance from your location to landmark A
as a vector. When you don’t know the distance, you can think of this vector as a unit vector
with direction only. Unit vector (e_a) means you will assume its magnitude is 1. Knowing the
angle of this vector from the x axis, however, you can determine the components of this unit
vector for i(x direction) and j(y direction). You might want to sketch the unit vector and it’s
components on your map. Use the relationship below to find the components of the unit
vector (e_a) to landmark A and the unit vector (e_b) to landmark B.

5. Now we will use the map edges to compare the distance of landmark A and your distance
from the map edge. Let’s assume your distance from the western edge of the map is x and your
distance from the southern edge of the map is y (you still don’t know where this is) - you’re
just making a variable for what you want to know. You can now assume that the ratio of these
distances is equal to the ratio of the components of the unit vector. rite out this equation filling
in the values that you know , but keep it in its present form. Do this for landmark B as well.

6. Look at your equations and determine how many unknowns you have. Also determine how
many equations you have. Could this help you find your location in some way ?

7. To solve your equations , put them in this format for solving simultaneous equations . You
can insert the values which you know from your map.

8. Now you may or may not remember an application of Cramer’s Rule (in connection with
determinates) which allows you to solve for x and y. It goes like this ...You can use this to
input your knowns, simplify , and solve for your unknowns - namely where are you ?

9. Depending on the units you chose (centimeters on your ruler or distance on the map itself),
these final values for x and y will give you the distance of your location to the edges of the
map. Now determine your location and what you are doing here.

10. Now that you know where you are, calculate the distance (d_a and d_b) to each of your two
landmarks. To do this, use the Pythagorean theorem for the distance between 2 points. Give
your answer with the correct digits.

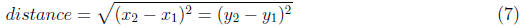
11. If you used your ruler graduations for your measurements, convert to map units by looking
at the scale of the map. For example if the map is 1:100,000, every centimeter on a map
corresponds to 100,000 cm in the field.

There is an advantage of recasting vectors in terms of their components because you can use
vector addition of the components to make the problem simpler. To add 2 vectors together,

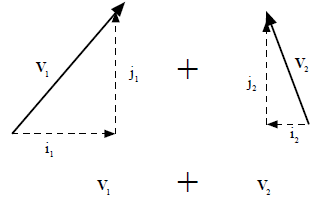
you can just add their components,

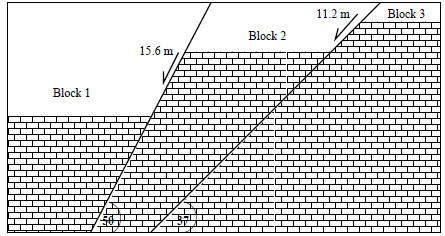
12. In the block diagram above, determine the total movement of block 1 relative to block 3.
To do this you can just add the slip vector () for fault 1 to the slip vector (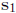) for fault 2. To
determine 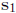use the rules for finding vector components. Find each of the two component
vectors i and j for each fault slip vector.

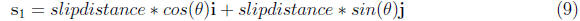
13. Add the components of each of these vectors as in equation 8. This will give you the
components of the final slip vector (remember you are still in ”component space”).

14. To determine the total slip distance of block 1 relative to block 2, use Pythagorean’s
theorem for a right triangle.

15. Find the equivalent fault dip (if this total slip occurred on one fault) by using the same
theory. This gives the fault dip, and slip magnitude for an equivalent fault that would show the
total displacement of block 1 relative to block 3.

C. Find the Distance Between Los Angeles and Miami)
How far is it between Los Angeles and Miami ? Determine the arc distance between these two
cities considering the curvature of the surface of the Earth. To do this, define your position
vector in 3 dimensions for a sphere considering your origin at the center of the Earth. Let the
z axis run up through the North Poke, the x axis pass through the equator at the Prime (or
Greenwich) Meridian and let the y axis pass along the equator to longitude 90° E (this is
somewhere near the longitude of eastern Tibet). Use these coordinates for your 2 points and
the radius of the Earth as 6370 km.

Los Angeles
Latitude: 34.05 ° N
Longitude: 118.22 ° W

Miami
Latitude: 25.45 ° N
Longitude: 80.15 ° W

To solve for z, x, and y in 3 dimensional Cartesian coordinates assume:

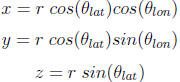
16. Determine the x, y, and z components for each of the 2 cities. Write the vector 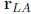and
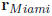in terms of each of 3 vectors for i ,j, and k.

17. To find the angle ( λ ) between 2 vectors use the dot product . Where 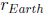  is the radius of
the Earth.

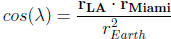
18. To determine the total distance in kilometers use your knowledge of converting degrees to
kilometers - or consider the circumference of the Earth and how many total degrees is in the
circumference.