Ljunggren's Approach to Specific Lacunary Results

Theorem (Ljunggren): Let n and m be integers with n > m > 0, and let 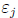∈ {1,−1} for
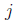∈ {1, 2}. Then the non-cyclotomic part of 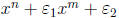is irreducible or identically 1.

Proof:
• The non- reciprocal part of f(x) = 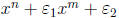is the same as the non-cyclotomic part of
f(x) (consider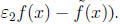

• Suppose w(x) ∈ 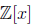with 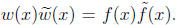The goal is to show w(x) = ±f(x) or
w(x) = ±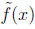. This will imply the non- reciprocal ( equivalently , non-cyclotomic) part of
f(x) is irreducible or 1.

• We can suppose w(x) has positive leading coefficient and m ≤n − m (the latter by using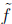
instead of f if necessary).

• Observe that w(0) ≠ 0 and w(x), 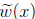, f(x), and 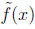have the same degree, namely n.

• Since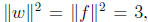 each coefficient of w (x) is either 1 or −1. Write w(x) = xⁿ +
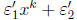where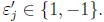

• We can suppose k≤ n − k.

• Note that

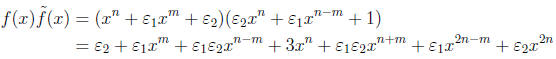
and

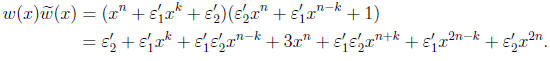
• Comparing the least two exponents above, 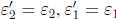,and k = m. Thus, w(x) = f(x).

Theorem (F. & Solan): Let f(x) = xⁿ + x^m + x^p + x^q + 1 be a polynomial with n > m > p >
q > 0. Then the non- reciprocal part of f(x) is either irreducible or 1.

Proof:
• Suppose w(x) ∈ 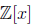with 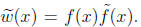The goal is to show w(x) = ±f(x) or
w(x) = ±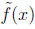

• In this case, we may further suppose w(x) is a 0, 1- polynomial (and do so). Write w(x) =
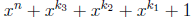with 0 < k₁ < k₂ < k₃ < n.

• By considering reciprocal polynomials if necessary , we consider m+q ≤n and k₁+k₃≤n.

• The condition 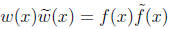implies

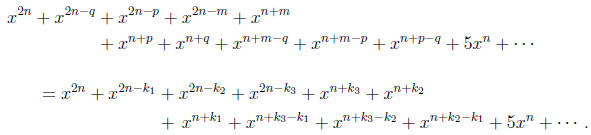
• Deduce 2n − k₁ = 2n − q so that k₁ = q.

• By adding exponents , deduce 14n + 2k₃ − 2k₁ = 14n + 2m − 2q so k₃ = m.

• Substitute and compare exponents to obtain

{2n − p, n + p, n + m − p, n + p − q} = {2n − k₂, n + k₂, n + k₃ − k₂, n + k₂ − k₁}.

• Comparing largest elements of these sets, deduce one of 2n−p and n+p must equal one of
2n − k₂ and n + k₂.

• If 2n − p = 2n − k₂ or n + p = n + k₂, k₂ = p and w(x) = f(x).

• If 2n − p = n + k₂ or n + p = 2n − k₂, then k₂ = n − p. Substituting and comparing
exponents , deduce

{n + m − p, n + p − q} = {n + k₃ − k₂, n + k₂ − k₁} = {m + p, 2n − p − q}.

If n + m − p = m + p, then n = 2p so that k₂ = n − p = p and w(x) = f(x). If
n + m − p = 2n − p − q, then n = m + q so that k₃ = m = n − q, k₁ = q = n − m, and
w(x) = 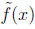.