High School Math Contest

A triple of positive integers x, y, z is called a Pythagorean Triple if these integers satisfy the equation

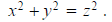
For example, (3, 4, 5) is a Pythagorean Triple. A Pythagorean Triple is said to be primitive if the integers are
relatively prime. That is, they have no common integer factor except 1. The triple (3, 4, 5) is also a primitive
Pythagorean Triple.

1. If (x, y, z) is a primitive Pythagorean Triple show that

 a. Exactly one of x and y is odd and hence that z must also be odd,
If both x and y are even that means z^2 must be even and thus so is z, which means that x, y,
and z are not relatively prime; they’re all divisible by 2. If both x and y are odd, then x^2+y^2
must be even. Note that this sum is not divisible by 4. However, since z^2 is even z must be
even and this forces z^2 to be divisible by 4, a contradiction. So the only alternative is that x and
y must have opposite parity, which forces z to be odd.

 b. Exactly one of x and y is divisible by 3,
If both x and y are divisible by 3 then so is z, which contradicts the relative primeness of x,
y, and z. If neither x nor y is divisible by 3, then x^2 and y^2 must have remainder 1 when divided
by 3. so their sum must have a remainder of 2 when divided by 3, but z^2 can only have
remainder 0 or 1, when divided by 3. Thus, exactly one of x and y is divisible by 3.

 c. Exactly one of x, y, and z is divisible by 5.
Again, since the three integers are relatively prime, not all of x, y, and z are divisible by 5.
If two of them are divisible by 5, then the third must also be divisible by 5, which we know
cannot happen. The last case to consider is if none of them are divisible by 5. However, the
square of any integer has remainder 1 or 4 when divided by 5: this means that the third must
have remainder 0, or 2, or 3 when divided by 5, a contradiction. The only case left is that one
in which exactly one of the three is divisible by 5.

2. Is there a Pythagorean triple of the form (2, y, z) ?

The answer is no. Suppose (2, y, z) is a Pythagorean triple. That is,

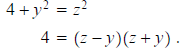
Since z-y and z+y are integers and are divisors of 4 they can take on the values of 1, 2, or 4 only. If
z-y is 1, then z+y=4. This means that z=5/2, a contradiction. If both factors are 2, we then have
z=2 and y=0, but Pythagorean triples consist of positive integers. Thus, there is no Pythagorean triple
of the form (2, y, z) .

3. If (x, y, z) is a Pythagorean triple then the isosceles triangles with sides of length 2x, z, z and 2y, z, z
have the same area.

The isosceles triangle with sides of length 2x, z, and z has area xy as does the isosceles triangle with
sides of length 2y, z, and z. The altitude of the first triangle is y, while the altitude of the second triangle is
x.

4. Let (x, y, z) be a Pythagorean triple. Let r be the radius of the inscribed circle of the right triangle with
sides x, y, and z.

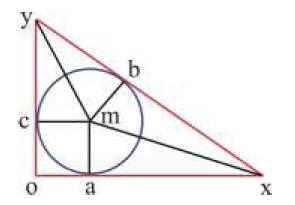
a. Show that r must be an integer with the value

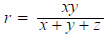
In the figure above we have oc=oa=mc=ma=mb=r, triangles mcy myb are
congruent as are triangles mbx and axm. Thus,

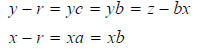
Thus, we have

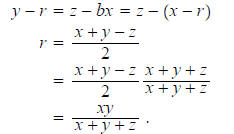
Since two of the three terms in the numerator of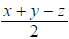are odd, the equation

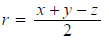
shows that r is indeed an integer.

b. Let n be any positive integer. Show that there is a right triangle whose sides have integer
length and whose inscribed circle has radius n.

From problem 6 below we see that if k is any odd integer greater than 1, then
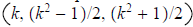is a Pythagorean triple. The inscribed circle for the corresponding
right triangle has radius

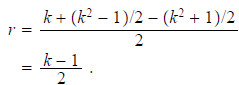
As k goes through the odd integers 3, 5, 7, …, the corresponding value of r goes through each
of the natural numbers. Note that this Pythagorean triple is also primitive.

5. If (x, y, z) is a Pythagorean triple, show there are integers m and n such that z^2+xy=m^2+n^2; show
that a similar statement is true for z^2-xy.

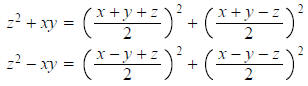
Note that one of x and y is odd as is z. Thus, all four numerators are even , which implies that each ratio is
an integer .

6. For any odd integer k show that there is a primitive Pythagorean Triple, (k, l, m) , such that
m=l+1. Your proof should be constructive. That is, given k how do you find l and m.
Note: (3, 4, 5) and (15, 112, 113) are both Pythagorean triples with the desired property.

Given k set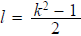and 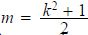Since k is odd both l and m are integers, and it is an easy
computation to verify that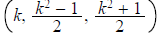is a Pythagorean triple whose second and third terms
differ by 1.

7. Suppose the λ is a positive rational number . That is, λ=m/n with m and n positive integers. Find
necessary and sufficient conditions on m and n such that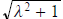is also rational.

A necessary and sufficient condition is that m and n are the smaller two integers in a Pythagorean
triple. Suppose first that there is a z ∈N such that m^2+n^2=z^2, then we have

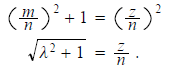
Conversely, suppose that 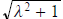is a rational number a/b in lowest terms . Then

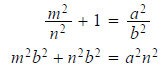
Since a and b are in lowest terms and b^2 divides a^2n^2 we know that b^2 divides n^2, which implies that b
divides n. Thus, there is a k such that n=bk, and we see that

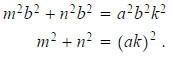
That is, m and n are the smaller two numbers of a Pythagorean triple.

8. Show that if (x, y, z) is a primitive Pythagorean Triple (assume that y is even) then there are integers r
and s of opposite parity such that

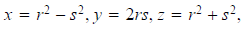
and the greatest common divisor of r and s is 1.

Since we have a primitive Pythagorean triple the integers x and z are relatively prime, which implies
that the integers z-x/2 and z+x/2 are also relatively prime. Remember, we are assuming that y is even,
which forces x and z to be odd. Thus ,we have

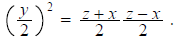
Since the integers z-x/2 and z+x/2 are relatively prime, and each divides the square of an integer, their
square roots must also be integers. That is

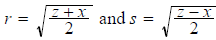are integers, and we have

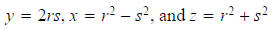
Since x and z are both odd r and s must be of opposite parity, and since x, y, and z have no common
divisors neither can r and s.

9. Prove that there is no isosceles right triangle with sides of integer lengths, but given any ∈>0, there is a
Pythagorean triple, such that the right triangle with side lengths given by the triple has the property that
the smaller of the non-right angles is within of ∈of π/4

Suppose we had an isosceles right triangle with sides of length a, a, and b. Then we have the
equation

2a^2=b^2,

which implies that sqrt(2)=b/a a rational number, but sqrt(2) is not rational. This contradiction tells us that an
isosceles right triangle cannot exist.

To see that we can get one of the acute angles of a right triangle as close as we want to 45°, we use
the result of problem 8.

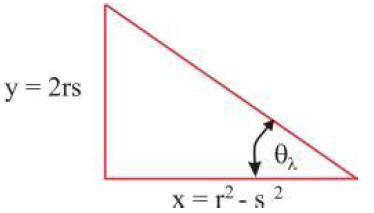
To have angle θ_λ close to π/4, we show that we can pick r and s so that its tangent is close to one.

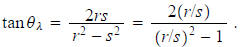
Let λ=r/s. Then we want to pick λ so that 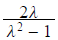is close to one. Suppose this ratio is equal to 1. Then
must equal 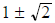. Since λ is the ratio of two positive integers, we want λ equal to 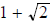. This can’t
happen for rational λ , but we can pick a sequence of rational numbers λ_n that converge to 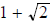. That
is, we can pick a sequence of positive integers r_n and s_n such that 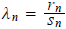is arbitrarily close to ,
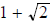which means that tanθ_λn is arbitrarily close to 1, and hence θ_λn is as close to π/4 as desired